Do granic wielu ciągów z logarytmami śmiało stosować można przekształcenia i wzory na logarytmy znane ze szkoły średniej. Na przykład:
Przykład na granicę ciągu z logarytmami
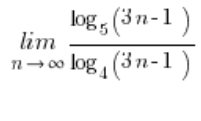
W sytuacjach, w których w logarytmach były różne podstawy i za bardzo nie dało się nic z tym zrobić sprowadzało się je do jednej podstawy ze wzoru: 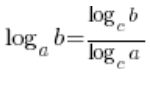 . W naszej granicy fajnie i dogodnie będzie za tą podstawę przyjąć:
. W naszej granicy fajnie i dogodnie będzie za tą podstawę przyjąć: ![]() . Będziemy mieli więc granicę ciągu:
. Będziemy mieli więc granicę ciągu:
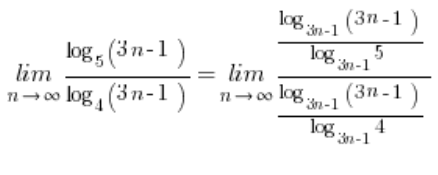
Wiemy, że ![]() , czyli w naszym wyrażeniu
, czyli w naszym wyrażeniu 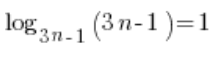 . Zatem:
. Zatem:
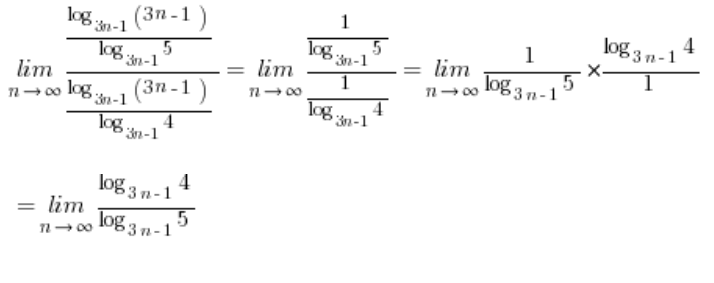
A to wyrażenie korzystając znowu ze wzoru ze szkoły średniej (tylko tym razem w drugą stronę) równe będzie 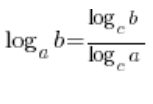 …
…
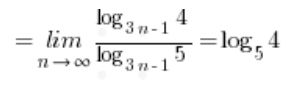
Co jest oczywiście wynikiem (liczbą niewymierną).
Obeszło się nawet bez stosowania jakiś metod na granice – wystarczyły same przekształcenia logarytmów ze szkoły średniej.
Chcesz wiedzieć więcej o obliczaniu granic? Polecam mój Kurs 🙂



4 Komentarzy
Karla
mam pytanie co do granicy ciągu lim n->plus nieskończoność log n gdyż w odp do zadania mam plus nieskończoność a w pewnych materiałach w \internecie znalazłam że powinno to byc minus nieskończoność i nierozumiem tej rozbieżności. Pozdrawiam
Krystian Karczyński
Powinno być plus nieskończoność.
Jeżeli w podstawie logarytmu jest liczba mniejsza od 1 (np. [pmath]log_{o,5}{n}[/pmath], wtedy dąży on do -[pmath]\infty[/pmath].
Jednaj w przypadku log n w podstawie logarytmu jest liczba 10 (jest to logarytm dziesiętny), zatem dąży on do +[pmath]\infty[/pmath].
matheavyk
zdaje się, że przedostatnie równanie jest błędne. b powinno być u góry, a – na dole
Krystian Karczyński
Tak, poprawiłem już (był błąd), przepraszam!!!