欧拉第一类替换

---

欧拉替换 – 这对谁有用？

在不定积分中的欧拉替换是在有理积分、三角积分和根式积分（或者按照某些分类：“非有理积分”）之后介绍的下一个主题。这意味着大多数学生可能不会有机会遇到它们，我在我的不定积分课程中也没有包括它们。

然而，仍然有相当一部分数学专业的学生，或者真的在数学上非常“强”的学生，需要面对欧拉替换，我邀请这些（以及感兴趣的）学生加入。我将讨论欧拉替换的所有三种类型（在这篇帖子中我将处理第一种类型），并为每一种做一个示例。

让我们开始吧。

我们用欧拉替换解决哪些积分？

我们用欧拉替换来解决以下类型的积分：

…即一些任意的关系 和 。所以可以将它们视为根式积分（“非有理积分”）的一种“延伸”。

我们用欧拉替换来解决那些无法更简单地解决的积分，当然。例如，积分：

是一个涉及 和 的关系的积分，但可以通过一个简单的替换 来非常容易地解决。所以在这些简单的积分中，我们不需要费劲用欧拉替换。

但让我们来看这个积分：

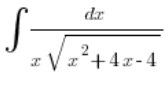
我们看到情况更为严重，先前熟悉的替换或（不能从中确定）不能解决问题。

我们需要新的武器。

欧拉替换 – 第一类

考虑到这个积分：

其中，

我们使用替换：

，然后对两边都进行平方，项相互抵消（这正是我们的目的），我们依次确定：

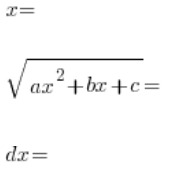
，用t表示，然后将其代入原积分中：

我们得到一个关于t的积分（如果里面还有任何x的话，那就是我们犯了错误），这是一个有理积分。

注意

值得一提的是，实际上许多学生只被教授了第一类欧拉替换，且仅用于以下类型的积分：

，即那些似乎

让我们通过一个例子来跟踪欧拉第一类替换的应用：

例子 1

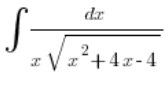
我们发现这是一个积分，涉及 和 的关系。不能简单地解决。而且 （ 是在 旁边的系数，在我们的例子中它等于 1）。

所以我们将使用欧拉第一类替换。

我替换：

也就是：

然后对两边都进行平方：

两边的 项相互抵消（这是每次都应该发生的）：

现在我们需要确定 , 和 （按这个顺序）。

我们从 开始：

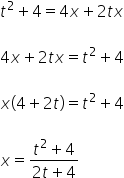
我们有 用变量 t 表示。现在轮到 ，即在我们的例子中：。

我们回到我们的第一个替换，其中有：

现在我们已经知道 （可以看出，顺序很重要，对吧？），因此我们可以写：

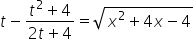
也就是：

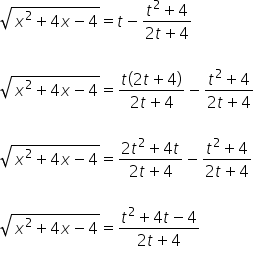
所以我们有 用变量 表示。

最后，我们通过对确定的 进行微分来得到 ：

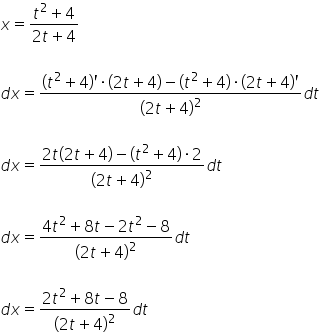
这样我们就确定了 。所以我们有：

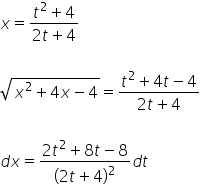
我们将这一切放入原始积分中：

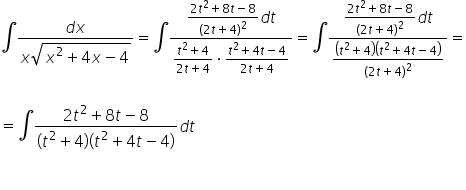
乍一看，这看起来像是无聊、繁琐但已知和有模式的有理积分（分解为简单分数，分母中的第二项还可以进一步分解）。通常情况下是这样，但在这个具体例子中，我们将有一些运气，避免了穿越3页A4纸的计算：

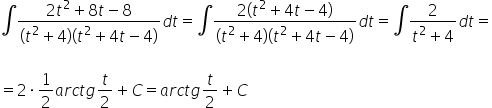
如何通过替换回到原来的表达式？我们一开始有：

因此显然：

所以我们的结果是：

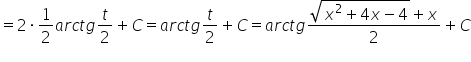
待续。 (我们还有其他两种欧拉替换，如果系数 不大于零会怎样？)。