齐次方程组（使用矩阵的秩求解解的数量）
Krystian Karczyński
eTrapez网站的创始人兼负责人。
波兹南理工大学（波兰）数学专业硕士。拥有多年数学家教经验。创建了第一个eTrapez课程，这些课程在波兰全国的学生中获得了巨大的流行。
居住在什切青（波兰）。喜欢森林散步、海滩放松和划独木舟。
齐次线性方程组是指所有常数项都等于0的方程组。它们看起来像这样：
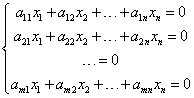
例如：
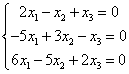
线性方程组的解的可能数量
让我们回顾一下，在每个线性方程组中有三种可能的情况：
- 方程组有一个解（当矩阵的秩等于增广矩阵的秩等于方程组中的未知数的数量：
） - 方程组有无穷多解（当矩阵的秩等于增广矩阵的秩并且小于方程组中的未知数的数量时：）
- 方程组无解（当矩阵的秩不等于增广矩阵的秩时）
增广矩阵是指在原矩阵中添加常数项列。在齐次方程组中，这将是一个全为零的列。在计算秩时可以直接去掉这一列，从而得到原矩阵。
在我们的例子中，原矩阵的秩为：
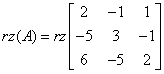
而增广矩阵的秩为：
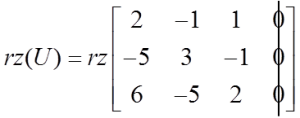
在示例中可以看到
并且可以看出这将永远如此，在每个齐次方程组中都是如此。
齐次线性方程组的解的可能数量
因此，在齐次方程组中，只会有1或2种情况。方程组总是有解，只是问题在于这是一个解还是无穷多个解。
让我们继续。
定义一个所谓的“零解”。我们将所有未知数的值都为零的解称为零解。
在讨论齐次方程组时，可以注意到：
零解始终是齐次方程组的解。
这很容易验证：如果将所有未知数都设为零，很明显，每个齐次方程组的方程都将得到满足，始终如此。
因此，如果我们知道齐次线性方程组有一个解（当
时），我们也知道这一定是零解。
如果我们知道齐次线性方程组有无穷多个解（当
时），我们知道方程组有零解，但除此之外还有一些非零解。
如果题目要求我们：“检查齐次方程组是否有非零解”，只需证明这是一个不定方程组，其中原矩阵的秩和增广矩阵的秩小于未知数的数量。
在某些方程组中，这很简单，例如这里：
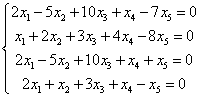
方程组的原矩阵有4行5列，因此它的秩最多为4。增广矩阵的秩也是如此——我们已经知道为什么。未知数的数量为5。因此可以立即断定方程组是不定的，并且该方程组存在一些非零解。
你在寻找大学或高中级别的数学家教吗？ 或者你需要一个课程来帮助你准备高考吗？
我们是eTrapez团队。我们以清晰、简单和非常详细的方式教授数学 - 甚至可以触及到最抗拒学习的人。
我们创建了用易懂的语言解释的视频课程，可以下载到电脑、平板或手机上。你只需打开视频，就像在家教课上一样，观看和聆听。无论是白天还是夜晚，任何时候都可以。
