Wzór na pochodną funkcji złożonej

Wzory na pochodne

Temat: Wzór na przyrost funkcji. Wzór na pochodną funkcji złożonej.

Streszczenie

Na tym wykładzie zajmiemy się potężnie wykorzystywanym w praktycznym liczeniu pochodnych (tzn. liczeniu z wzorów, a nie z definicji). Jest to oczywiście wzór na pochodną funkcji złożonej:

Tak się jakoś śmiesznie składa, że wzór – na każdym kroku stosowany – jest jednocześnie najmniej zrozumiały i w ogóle z reguły pomijany. Bierze się to stąd, że o wiele łatwiej nauczyć się po prostu, jak w praktyce obliczać te pochodne (z funkcji złożonej), niż wprowadzać do tego jakiś teoretyczny wzór.

Za chwilę jednak objaśnimy, jak “działa” ten wzorek i w sposób ścisły go udowodnimy. Skorzystamy przy tym z innego twierdzenia – o przyroście wartości funkcji i z oznaczeń , jakie wprowadziłem na poprzednim wykładzie (przypomnę je jeszcze).

Dowód przeprowadzam raz jeszcze tak, jak w książce Fichtenholz’a. Przy okazji, jeśli naprawdę pasjonujesz się matematyką (a ściślej: analizą matematyczną) MUSISZ mieć tą 3 tomową książkę, wpisz w Google czy Allegro – Fichtenholz, każdy wie o co chodzi, nie ma możliwości pomyłki.

Zaczynajmy zatem…

Funkcje złożone. Pochodne funkcji złożonych.

Z funkcjami złożonymi powinniśmy się już zetknąć w szkole średniej. Są to funkcje, w których argumentem jakiejś funkcji nie jest taki sobie zwykły ‘x’, jak Pan Bóg przykazał, tylko jakaś inna funkcja.

Na przykład:

Ta funkcja jest złożona. Argumentem funkcji sinus nie jest x (wtedy była by to prosta funkcja  ), tylko jakaś inna funkcja, a konkretnie – .

Funkcje złożone bywają bardziej podstępne, na przykład:

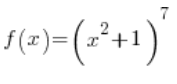
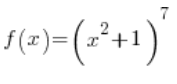
Tutaj potrzeba już bardziej wprawnego oka, żeby zauważyć, że mamy jest to funkcja , w której zamiast argumentu jest wstawiona funkcja .

Funkcję złożoną f, której argumentem jest jakaś inna funkcja g można przedstawić symbolem:

Ma to sens, prawda? f liczona nie z x, tylko z innej funkcji: g(x).

Jak wiemy, pochodną z funkcji złożonej liczy się ze wzoru:

Jak go rozczytać? Ano tak: pochodna z funkcji f, w której argumentem jest funkcja g równa jest pochodnej z funkcji f (argumentem tej pochodnej jest funkcja g), przemnożonej przez pochodną funkcji g.

Najlepiej załapać to na przykładzie. Weźmy naszą funkcję złożoną:

Podstawa to orientacja, która funkcja jest która, to znaczy, argumentem jakiej funkcji jest która funkcja, to znaczy która funkcja ze wzoru to nasza funkcja f (można też ją nazwać: “funkcja zewnętrzna”), a która to funkcja g (można też powiedzieć o niej: “funkcja wewnętrzna”). Nasza funkcja f w tym przykładzie to funkcja sinus, a jej argumentem jest funkcja g.

Zgodnie ze wzorem: , pochodna funkcji równa będzie pochodnej funkcji sinus (czyli cosinus), której argumentem jest funkcja g=lnx (czyli będziemy mieli cosinus z lnx) razy pochodna funkcji lnx (czyli ):

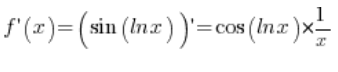
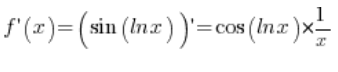
Można zapisać ją ładniej:

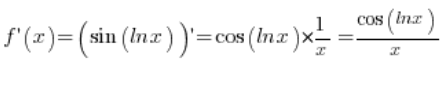
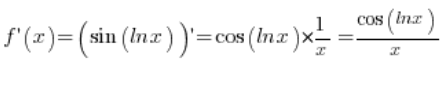
I tyle 🙂

Zajmiemy się teraz formalnym udowodnieniem naszego wzorku. Najpierw udowodnimy jednak pomocniczo…

Twierdzenie o przyroście wartości funkcji

Jak wiemy już z poprzedniego wykładu, przyrost wartości funkcji () w dowolnym punkcie   można zapisać jako:

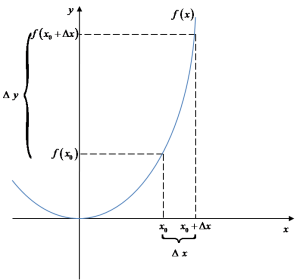
Widać to wprost z rysunku:

Wzór na przyrost wartości funkcji w punkcie można jednak zapisać również inaczej, w nie tak bardzo oczywisty sposób:

Twierdzenie

Jeśli funkcja f(x) ma w punkcie skończoną pochodną, to przyrost wartości tej funkcji w tym punkcie można przedstawić jako:

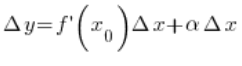
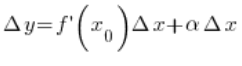
gdzie  jest wartością zależną od i wraz z   dążącą do zera.

Dowód

Zauważmy, że zgodnie z definicją pochodnej i tego, czym jest  (patrz wyżej):

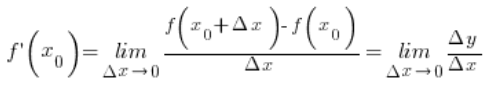
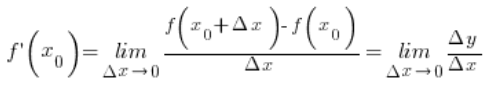
Jeżeli przyjmiemy więc, że:

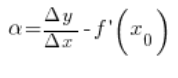
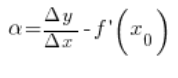
Widzimy, że zależy od i biorąc będziemy mieli (bo pokazaliśmy wyżej, że ).

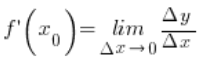
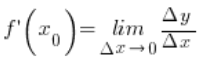
Tak obrana ma więc warunki określone w zadaniu.

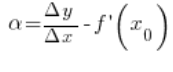
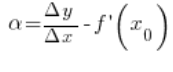
Obie strony równania mnożę przez :

Przenoszę stronami i mam:

Wyprowadziliśmy więc w ten sposób wzór na przyrost wartości funkcji z twierdzenia, co kończy dowód.

Twierdzenie o przyroście funkcji wykorzystamy w dowodzie wzoru na pochodną funkcji złożonej.

Twierdzenie o pochodnej funkcji złożonej

Pochodna funkcji złożonej (przy spełnionych założeniach dotyczących istnienia pochodnych funkcji w punkcie) dana jest wzorem:

Dowód

Dla przyrostu argumentów otrzymamy pewien przyrost wartości funkcji g: i pewien przyrost wartości funkcji f: . Zauważmy teraz, że przyrost wartości funkcji g jest jednocześnie przyrostem argumentów dla funkcji f (bo wartości funkcji g są argumentami funkcji f).

Wykorzystując nasze twierdzenie o przyroście wartości funkcji (udowodnione wyżej) dla funkcji f mamy:

we wzorze z twierdzenia zastąpiłem – bo argumentami funkcji f są wartości funkcji g, a nie x-sy.

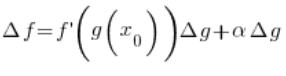
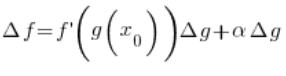
Dzielimy obie strony przez i mamy:

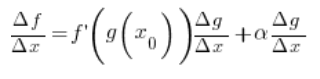
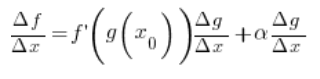
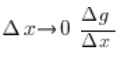
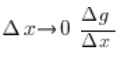
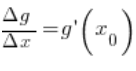
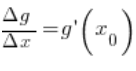
Biorąc teraz równe jest z definicji wartości pochodnej funkcji g w punkcie , .

Składnik: dąży więc do zera, bo samo dąży do wartości pochodnej funkcji g, a dąży do zera (zgodnie z twierdzeniem o przyroście funkcji), jedno zaś przemnożone przez drugie dąży do zera.

Mamy zatem (przechodząc do granicy przy ):

Co należało dowieść.

KONIEC

Pisząc tego posta korzystałem z…

1. “Rachunek różniczkowy i całkowy. Tom I.” G.M. Fichtenholz. Wyd. 1966.

Kliknij tutaj, aby przypomnieć sobie, jak wyprowadzić wzory na właściwości pochodnych (poprzedni Wykład) <–

Kliknij tutaj, aby powrócić na stronę z wykładami o pochodnych