Derivative formulas
Topic: Formula for function’s increment. Chain rule.
Summary
In this lecture we will deal with the powerful practical use of calculating derivatives (i.e. calculating from formulas, not from definitions). This is, of course, the chain rule:

It so happens that the formula above – used at every step – is at the same time the least understandable and generally omitted. This is because it is much easier to simply learn how to calculate these derivatives (from the chain rule) in practice than to introduce some theoretical formula.
However, in a moment we will explain how this formula “works” and we will prove it. To do this, we will use another theorem – about the increase in the value of a function and about the markings![]()
![]()
I carry out the proof as it has been shown in Fichtenholz’s book (“Differential and integral calculus. Volume I.” GM Fichtenholz. Ed. 1966.). By the way, if you are really passionate about mathematics (or more precisely: calculus) you MUST have this 3-volume book, just type Fichtenholz in Google or Amazon, there is no possibility of mistake.
So let’s get started…
Function composition. Derivatives of functions compositions.
We should already encounter functions compositions in high school. These are functions in which the argument of a function is not an ordinary ‘x’, but some other function.
For example:
![]()
![]()
![]()
![]()
This is function composition. The argument of the sine function is not x (as it would be in a simple function![]()
![]()
![]()
![]()
Function composition can be more hidden, such as:
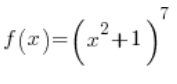
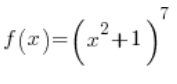
Here we need a more experienced eye to notice that this is a function ![]()
![]()
![]()
![]()
![]()
![]()
A function composition ‘f’ whose argument is some other function ‘g’ can be writen like this:
![]()
![]()
![]()
It makes sense, right? f is calculated not from x, but from another function: g(x).
As we know, the derivative of a function composition is calculated using the formula:






How to read it? Well, yes: the derivative of a function f, in which the argument is the function g, is equal to the derivative of the function f (the argument of this derivative is the function g), multiplied by the derivative of the function g.
It’s best to understand this with an example. Let’s take our function composition:
![]()
![]()
![]()
![]()
The most important thing is to get which function is in which, that is, the argument of which function is which function, that is, which function from the formula is our function f (you can also call it: “external function”) and which is function g (you can also say about it: “internal function”). Our f function in this example is the sine function and its argument is the g function.
According to the formula:





![]()
![]()
![]()
![]()
![]()
![]()
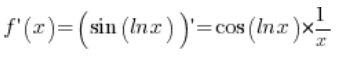
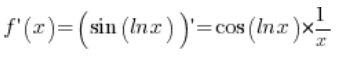
You can write it nicer:
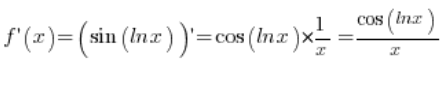
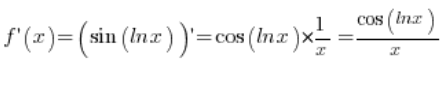
And that’s it 🙂
We will now formally prove our formula (chain rule). But first, let’s prove something helpful…
Increment theorem
As we already know from the previous lecture, the increase in the value of the function (![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
This can be seen directly from the drawing:
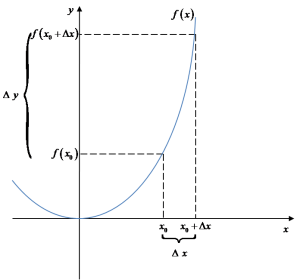

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
However, it can also be written differently, in a not so obvious way:
Proposition
If the function f(x) has at point ![]()
![]()
![]()
![]()
![]()
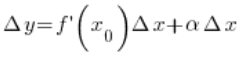
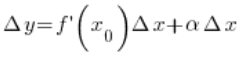
Where![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Proof
Note that according to the definition of derivative and ![]()
![]()
![]()
![]()
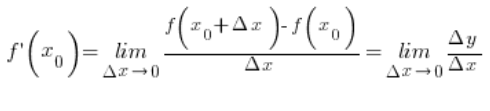
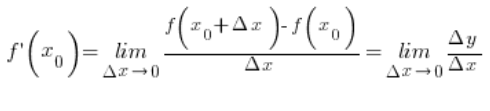
So if we assume that:
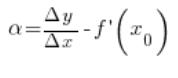
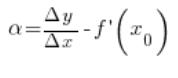
We see that![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
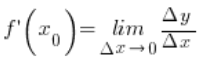
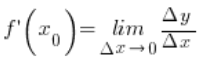
Such ![]()
![]()
![]()
![]()
![]()
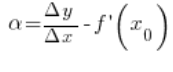
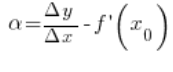
I multiply both sides of the equation by![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
I adjust the equation little bit more and I have:
![]()
![]()
We have thus derived the formula for the increase in the value of the function from the proposition, which ends the proof.
We will use the increment theorem in the proof of the formula for the derivative of a composition.
Theorem on the derivative of a composite (chain rule)
Derivative of a composite function![]()
![]()
![]()






Proof
For arguments increment ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Using our function increment theorem (proven above) for the function f we have:
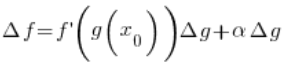
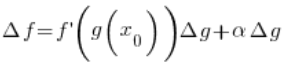
I replaced ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We can divide both sides by ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
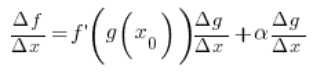
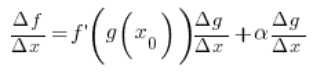
Taking now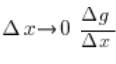
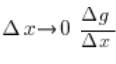
![]()
![]()
![]()
![]()
![]()
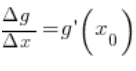
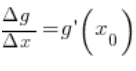
Component:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
So we have (converging to the limit at![]()
![]()
![]()






What needed to be proven.
END
While writing this post, I used…
1. “Differential and integral calculus. Volume I.” GM Fichtenholz. Ed. 1966.
Click here to review how to derive formulas for derived properties (previous Lecture)< —

