Достатня умова існування екстремуму функції

Екстремуми Функції Лекція 7

Тема: Достатня умова існування ек стремуму функції (зміна знаку похідної).

Зведення

Як з’ясувалося на попередній лекції, той факт, що похідна функції в точці дорівнює 0, не обов’язково означає, що сама функція досягає в цій точці екстремуму. Тут ми тому обговоримо, які умови достатні, щоб функція досягала екстремуму в якійсь точці.

Достатні умови існування екстремуму

Припустимо, що в певному оточенні точки $x_0$ функція $f \left(x \right)$ має скінченну похідну $f' \left( x \right)$ :

Якщо в цьому оточенні $x_0$ зліва від $x_0$ значення похідної функції є додатними, а справа від $x_0$ від’ємними – тоді функція приймає максимум в точці $x_0$
Якщо в цьому оточенні $x_0$ зліва від $x_0$ значення похідної функції є від’ємними, а справа від $x_0$ додатними – тоді функція приймає мінімум в точці $x_0$

Дійсно, відповідно до Леми про монотонність функцій, введеної на попередній лекції, якщо похідна функції приймає додатні значення, це означає, що функція зростає. Якщо ж похідна приймає від’ємні значення, це означає, що функція зменшується.

Отже, якщо похідна “змінює знак”, це також означає зміну монотонності функції , наприклад, у випадку 1.

Похідна зліва від є додатною, а справа від’ємною. Це означає, що функція зростає зліва від і зменшується справа. Виглядати це має приблизно так: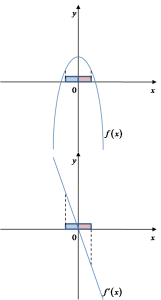
На вищенаведеному графіку ми бачимо графік функції (нагорі) та її похідної . Видно, що в “лівому” оточенні точки (позначено синім) похідна приймає додатні значення, а функція зростає. У “правому” оточенні точки (позначено червоним) похідна приймає від’ємні значення, а функція зменшується.