У складніших задачах з визначених інтегралів, завжди варто залишатися пильним – завдання, яке здається дуже складним, можна вирішити простою формулою з середньої школи.
Завдання на об’єм тіла обертання
Скажімо, нам потрібно обчислити об’єм тіла, утвореного шляхом обертання кривої:
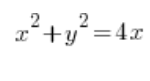
обертається (добре, нехай буде “ротується”) навколо осі OX. Кілька організованих рухів, відомих зі школи…
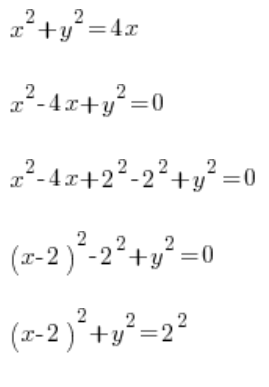
…і ми розуміємо, що наша крива просто маленьке коло з центром у точці (2,0) і радіусом 2. Що далі? Виводимо y з формули і просуваємо визначений інтеграл: 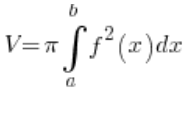 ?
?
Рішення
Ні… Зупинимося на мить. Вдихнімо повітря. Подумаймо. Маленьке колечко… Воно обертається… Що у нас вийде в результаті такого обертання? Звісно, куля. Формулу об’єму кулі ми знаємо ще з середньої школи:
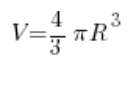
Радіус нам вже відомий (дорівнює двом), це означає:
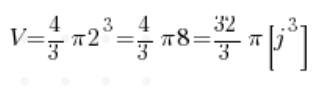
І ось ми маємо відповідь, навіть не торкаючись інтегралів 🙂


