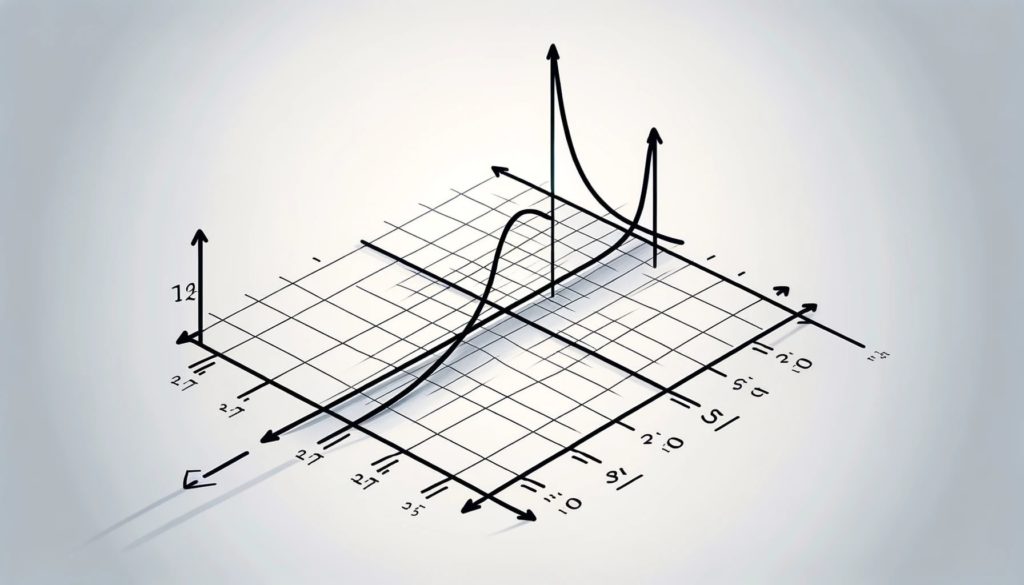
Зв’язок між горизонтальними та похилими асимптотами такий: горизонтальні асимптоти є спеціальним випадком похилих асимптот. Кожна горизонтальна асимптота тому є похилою, але не кожна похила є горизонтальною.
Це можна та слід використовувати, щоб спростити обрахунок асимптот функції. Існують два основні підходи до цієї теми:
1. Спочатку рахуємо горизонтальні асимптоти
Цей підхід показаний у моєму Відео Курсі з вивчення поведінки функцій.
Умова для існування горизонтальної асимптоти функції є:
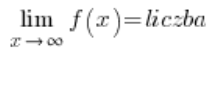 або
або 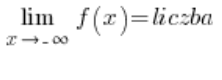
Якщо з’являються горизонтальні асимптоти, ми більше не рахуємо похилі (адже це так, ніби похилі вже визначені – пам’ятайте, що горизонтальні це тип похилих). Однак, якщо горизонтальні асимптоти не з’являються, тоді у нас є проблема – ми мусимо перерахувати похилі асимптоти.
Звичайно, ситуація трохи складніша: горизонтальна асимптота може “з’явитися” в ![]() , а “не з’явитися” в
, а “не з’явитися” в ![]() . У такому випадку ми не досліджували б існування похилої асимптоти в
. У такому випадку ми не досліджували б існування похилої асимптоти в ![]() (бо вона вже там з’явилася), але нам би довелося досліджувати її наявність в
(бо вона вже там з’явилася), але нам би довелося досліджувати її наявність в ![]() .
.
2. Спочатку рахуємо похилі асимптоти
…а потім горизонтальні асимптоти з’являться (або ні) автоматично; нам лише потрібно правильно інтерпретувати відповіді. Цей підхід я не показую у своєму курсі. Недолік полягає в тому, що умови існування похилої асимптоти функції трохи складніші:
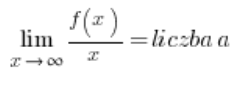 і
і 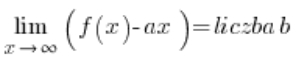
або:
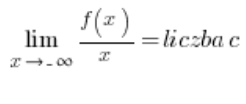 і
і 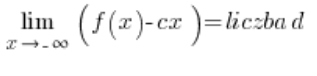
…і перевага в тому, що після їх обчислення не потрібно рахувати нічого більше. Якщо умови виконані і число ![]() (або
(або ![]() ) з умов на існування похилої асимптоти вийде дорівнює
) з умов на існування похилої асимптоти вийде дорівнює ![]() , то це означає, що похила асимптота насправді є горизонтальною.
, то це означає, що похила асимптота насправді є горизонтальною.
Щоб додатково спростити роботу, можна відразу розрахувати:
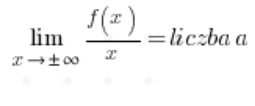 і
і 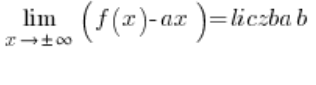
А розділити обчислення умов для ![]() і
і ![]() тільки тоді, коли це буде необхідно (коли це зробить різницю у результаті, чи �
тільки тоді, коли це буде необхідно (коли це зробить різницю у результаті, чи �
x прагне до ![]() , чи до
, чи до ![]() ).
).