Однорідні системи рівнянь (кількість розв’язків за допомогою рангу матриці)
Krystian Karczyński
Засновник та керівник сервісу eTrapez.
Магістр математики Познанської Політехніки (Польща). Репетитор з математики з багаторічним досвідом. Творець перших Курсів eTrapez, які здобули величезну популярність серед студентів у всій Польщі.
Живе у Щецині (Польща). Любить прогулянки лісом, відпочинок на пляжі та каякінг.
Однорідні лінійні системи рівнянь – це такі системи, у яких всі вільні члени дорівнюють 0. Вони виглядають так:
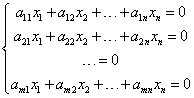
Наприклад:
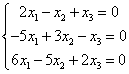
Можлива кількість розв’язків у системах лінійних рівнянь
Пригадаймо, що в кожній системі лінійних рівнянь можливі три ситуації:
- Система має 1 розв’язок (коли ранг матриці головної = ранг матриці доповненої = кількість невідомих у системі:
) - Система має нескінченну кількість розв’язків (коли ранг матриці головної = ранг матриці доповненої і менше кількості невідомих у системі )
- Система не має розв’язків (коли ранг матриці головної не дорівнює рангу доповненої матриці)
Доповнена матриця – це головна матриця з доданим стовпцем вільних членів. У випадку однорідної системи це буде стовпець з нулями. Під час обчислення рангів її можна просто викреслити й отримати таким чином тільки головну матрицю.
У нашому прикладі ранг головної матриці дорівнює:
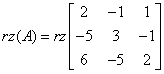
А ранг матриці доповненої:
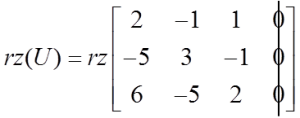
На прикладі видно, що 
і видно, що так буде завжди, у кожній однорідній системі.
Можлива кількість розв’язків у однорідній лінійній системі
Отже, в однорідних системах рівнянь можливі тільки ситуації 1 або 2. Система завжди матиме розв’язки, питання тільки в тому, чи це буде 1 розв’язок, чи нескінченна кількість розв’язків.
Йдемо далі.
Визначимо щось таке, як “нульовий розв’язок”. Нульовим розв’язком ми назвемо такий розв’язок, у якому значення всіх невідомих дорівнюють 0.
Говорячи про однорідні системи рівнянь, можна помітити, що:
Нульовий розв’язок завжди є розв’язком однорідної системи.
Це легко перевірити: якщо для всіх невідомих у рівняннях підставити нулі, ясно видно, що кожне рівняння однорідної системи буде виконане, завжди і в кожній однорідній системі.
Якщо ми знаємо, що однорідна система лінійних рівнянь має 1 розв’язок (а так є, коли 
), то ми також знаємо, що це точно нульовий розв’язок.
Якщо ж ми знаємо, що однорідна система лінійних рівнянь має нескінченну кількість розв’язків (а так є, коли 
), то ми знаємо, що система має нульовий розв’язок, але окрім нього ще якісь ненульові розв’язки.
Якщо в задачі маємо завдання: “перевірте, чи має однорідна система ненульові розв’язки”, достатньо показати, що це невизначена система, у якій ранг головної матриці та доповненої матриці менший за кількість невідомих.
У деяких системах це дуже просто, наприклад тут:
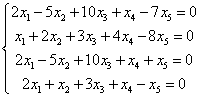
Головна матриця системи мала б 4 рядки та 5 стовпців, отже її ранг буде щонайбільше 4. Ранг доповненої матриці такий самий – ми вже знаємо чому. Кількість невідомих дорівнює 5. Тому відразу можна стверджувати, що система невизначена і що існують деякі ненульові розв’язки цієї системи.
Шукаєте репетитора з математики для університетського рівня або школи? А може вам потрібен курс, який підготує вас до вступних іспитів?
Ми - команда eTrapez. Ми вчимо математику ясно, просто і дуже детально - дістанемося навіть до найбільш відсторонених від знань.
Ми створили курси відео зрозумілою мовою для завантаження на комп'ютер, планшет або телефон. Вмикайте запис, дивіться і слухайте, як на репетиторстві. У будь-який час дня та ночі.
