Maturzyści pytają, eTrapez odpowiada. Wyprowadzenie wzoru na wysokość w trójkącie prostokątnym.
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Ten post poświęcony jest gościnnie fragmentowi zadania maturalnego, o który przesłał mi na maila pewien maturzysta. Warto jednak sobie zerknąć z ciekawości i nie powtarzać już nigdy więcej, że matematyka na studiach jest trudniejsza niż rozszerzona w szkole średniej.
🙂
Kawałek Zadania
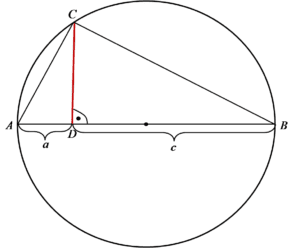
Mamy następującą sytuację:
Należy pokazać, że zaznaczony na czerwono odcinek ma długość 
. Całość oczywiście jest tylko malutkim fragmentem całego zadania, zgadnijcie na co? Na ciągi oczywiście 🙂
No więc można tu skorzystać z często wykorzystywanego w zadaniach z wysokością trójkąta prostokątnego patentu na “ulubione” przez wszystkich maturzystów trójkąty podobne.
1. Trójkąty 
(ten najmniejszy) i 
(ten największy, wpisany w okrąg) są podobne (mają 2 takie same kąty: prosty i <DAC, czyli trzeci kąt też jest taki sam, czyli mamy KKK). Trójkąty 
(ten średni) i (ten największy znowu) też są podobne (mają 2 takie same kąty: prosty i <CBD, czyli trzeci kąt też jest taki sam, czyli znowu mamy KKK). Jeśli trójkąty: i są podobne do , to są także podobne do siebie i o to chodziło i to zauważamy:
jest podobny do
2. Jeżeli te trójkąty są podobne, to stosunki ODPOWIADAJĄCYCH sobie boków będą równe. Oczywiście dobieramy te stosunki, zawierające zaznaczony na czerwono odcinek, którego długość oznaczmy powiedzmy jako 
.
W trójkącie stosunek boku NAJKRÓTSZEGO przez bok ŚREDNI będzie równy:
W trójkącie stosunek boku NAJKRÓTSZEGO przez bok ŚREDNI będzie równy:
Skoro trójkąty są podobne, to zachodzi równość:
3. Z równości wyznaczamy h, czyli długość zaznaczonego na czerwono odcinka. Mnożymy na krzyż jak to w proporcjach bywało i mamy:
Czyli:
Czyli to co mieliśmy dokładnie pokazać na początku. BINGO.
Morał wynosimy taki: wyznaczając wysokość w trójkącie prostokątnym (tą opadającą na przeciwprostokątną of course) często trzeba posłużyć się podobieństwem trójkątów, tak jak wyżej.
I jeszcze taki, że matematyka rozszerzona w szkole średniej potrafiła naprawdę ukąsić. Dopiero na studiach można odetchnąć 🙂
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Można było to też policzyć układając 3 równania Pitagorasa i z tych równań wyznaczyć h
Pewno można. Ja w średniej też wszystko układami równań i Pitagorasami rozwalałem. No może prawie wszystko.
Rany, dziękuję, że tak profesjonalnie potraktował pan moje pytanie. Jestem za to ogromnie wdzięczny. Z kolegą doszliśmy jednak o wiele szybciej, czemu ten odcinek jest równy pierwiastkowi z ac. Otóż kąt ACB jako oparty na średnicy jest prosty, a wysokość poprowadzona z wierzchołka kata prostego dzieli przeciwległy bok na odcinki w taki sposób, że h^2 = a*c . Ten wzór jak przypuszczam wynika pewnie z podobieństwa, tak jak pan to wykazał. Jeszcze raz wielkie dzięki…
Łeeee… Z wzorem nie ma zabawy 🙂