Podczas nagrywania Lekcji 7 mojego Kursu Pochodnych i Badania Przebiegu Zmienności Funkcji mocno uświadomiłem sobie pewną wskazówkę, która może pomóc Wam w nauce matematyki na studiach.
Typowe i wyjątkowe przypadki
Atakując na początku jakieś zagadnienie (na przykład właśnie tą monotoniczność) skup się mocno na zrobieniu kilku – kilkunastu przykładów typowych, standardowych i sztampowych, w przypadku zastosowań pochodnych do badania monotoniczności mogły by to być jakieś tam:
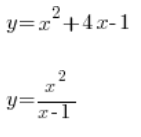
albo klasyk:
![]()
Właściwie na początku powinieneś robić tylko takie przykłady. Na tym etapie oprzyj się pokusie próbowania odpowiadania sobie od razu na wszystkie możliwe wątpliwości i pytania, taki jak: „Co będzie, jak dziedzina pochodnej będzie różna od dziedziny funkcji?”, albo co będzie, kiedy pochodna nie będzie miała miejsc zerowych. Po prostu odłóż je na później.
Kiedy otrzaskasz się w temacie na prostych i standardowych przykładach, powoli komplikuj sobie życie wprowadzając przykłady trudniejsze i problemowe. A jeżeli z tego powodu „skończy Ci się czas” i będziesz musiał iść na kolokwium bez gruntownego przerobienia każdego możliwego przypadku, to i tak lepiej, żebyś tam poszedł z wiedzą pewną odnośnie standardów, niż niepewną i nieutrwaloną, ale teoretycznie „ogarniającą wszystko”.
Powodzenia z pochodnymi funkcji!
P.S.
Na deser zamieszczam wykresy wszystkich trzech wspomnianych w poście funkcji, wraz z ich pochodnymi pierwszego i drugiego rzędu i tabelkami (niepełnymi) zmienności.
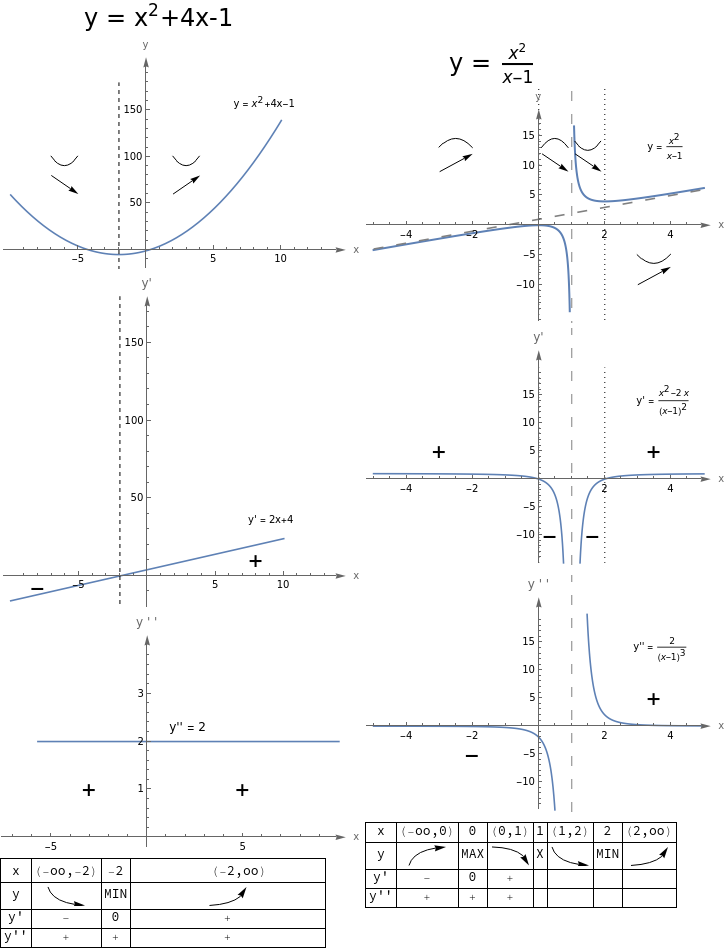
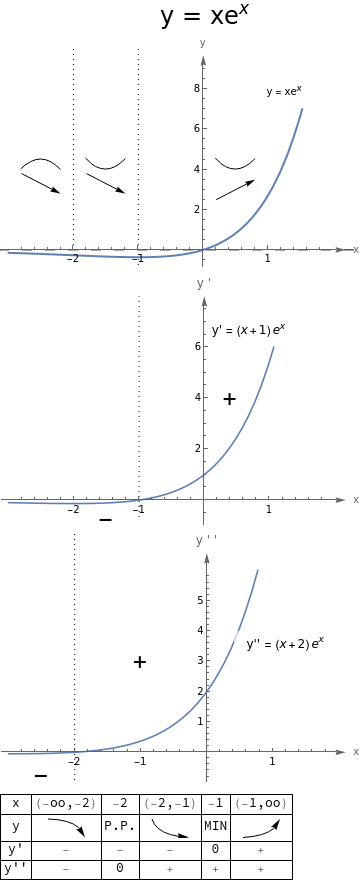

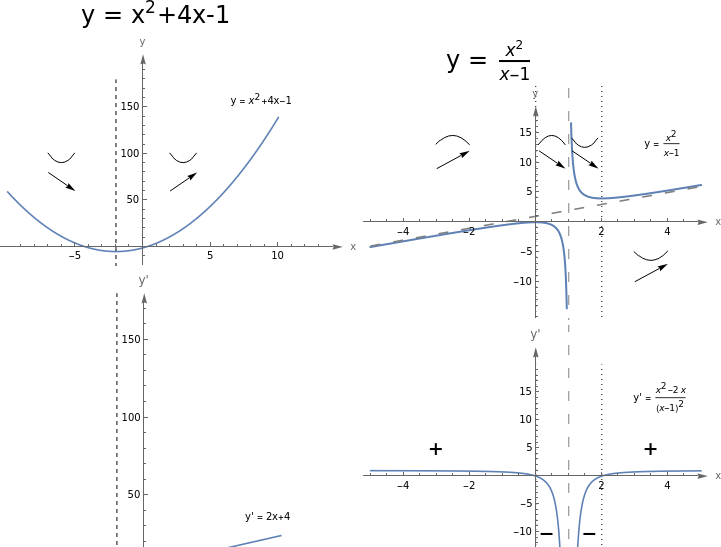

16 Komentarzy
Natalia
A co z przykładem f(x)=(8-x^2)*(pierwiastek trzeciego stopnia z x^2)? Jak tutaj będzie wyglądać monotoniczność i ekstrema?
Jerzy
Zabawę z analizą matematyczną skończyłem w roku 1963. Obecnie będąc na emeryturze postanowiłem, korzystając z Pana świetnych wykładów i poglądowych filmów ,
rozruszać szare komórki. A tu klops! Siedzę już trzeci wieczór i nie mogę sobie poradzić z wydawało by się prostą rzeczą.Chodzi o wyznaczenie ekstremum warunkowego funkcji wielu zmiennych. Może Pan byłby uprzejmy i pomógł mi rozwiązać to zadanie. A oto treść: wyznacz ekstremum warunkowe funkcji :
f(x,y,z)=sin(x)sin(y)sin(z) przy warunku x+y+z = pi/2; x,y,z>0
Kamil Pietruszewski
Panie Jerzy, funkcja f to niestety funkcja nie jednej, ale trzech zmiennych. Znajdowanie ekstremow takich funkcji jest troszke inne, w szczegolnosci, gdy na funkcje nalozony jest dodatkowy warunek. Proponuje zerknac gdzies i poczytac o metodzie tzw. Mnożników Lagrange’a 🙂
Marcin
Witam, mam pytanie. Otóż , jak zbadać monotoniczność takiej funkcji (za pomocą pochodnych). f(x)=(x-2)^5 * (2x+1)^4 ..oraz określić kiedy jest rosnąca , a kiedy malejąca. Pozdrawiam.
Krystian Karczyński
Witam, rozwiązuję ten przykład w tym filmiku, zapraszam:
mania
W kursie nie spotkałam się z podobnym przypadkiem, natomiast na egzaminie tak. W badaniu monotoniczności funkcji, dziedzina funkcji = R, natomiast dziedziną pochodnej to już tylko R dodatnie. Moje pytanie brzmi, czy kiedy piszę odpowiedź odnośnie monotoniczności funkcji, to uwzględnić w niej przedział od -nieskończoności do 0? Czy skoro nie ma go w pochodnej to znaczy , że funkcja pierwotna również nie rośnie, ani nie maleje w tym przedziale. Z góry dziękuję za szybka odpowiedź (jutro egzamin ). Pozdrawiam
Krystian Karczyński
O rety, a co to za funkcja?
mania
może coś pokręciłam jednak. x^2x
Krystian Karczyński
Niestety, to jest dosyć wyjątkowa funkcja, jej dziedziną jest zbiór R dodatnie (już na starcie…). Ma to sens, bo inaczej np. dla x=-\frac{1}{4}mielibyśmy pierwiastek z liczby ujemnej.
Niech Pani zerknie na opis tej funkcji w WolframAlpha:
x^(2x)
I na jej wykres:
Michał
Mam pytanie:
W kursie pochodnych- badanie monotoniczności funkcji. Powiedział Pan, że nie można dzielić obie strony przez liczbę ujemną gdy szukaliśmy miejsc zerowych danej funkcji (czyli gdy przyrównujemy ją do zera). I moje pytanie jest- dlaczego? Pierwszy raz spotkałem się z taką informacją.
Krystian Karczyński
Tak, to jest taki mój prywatny „patent”. Dla samego wyznaczenia miejsc zerowych funkcji dzielenie przez liczbę ujemną równości nie ma oczywiście żadnego znaczenia.
Natomiast takie dzielenie może zmienić wygląd wykresu, a przecież miejsca zerowe liczymy tylko po to, żeby narysować przybliżony wykres.
Na przykład:
Mamy (teoretycznie) obliczoną pochodną {y}'={{x}^{2}}
Wiemy oczywiście, że jej wykresem jest parabola z ramionami skierowanymi do góry, pochodna jest dodatnia dla wszystkich xróżnych od 0, wniosek z tego taki, że funkcja ynie osiąga ekstremum w zerze (pochodna „nie zmienia” znaku).
Jednak powiedzmy, że nie mamy o tym pojęcia i liczymy według sztywnego schematu z Kursu:
Liczymy jej miejsca zerowe:
{{x}^{2}}=0
Podzielenie obu stron tego równania przez xoczywiście nie zmieni w żaden sposób miejsc zerowych pochodnej, jednak drastycznie zmieni jej wykres, bo dostaniemy:
x=0
Dalej stosując się do reguł z Kursu narysowalibyśmy przybliżony wykres, którym była by prosta, wyszła by nam pochodna zmieniająca znak w zerze i wszystko by się posypało.
Dlatego właśnie w Kursie wprowadziłem tą ścisła i z kosmosu wziętą regułę nie dzielenia przez wartości, które mogą być ujemne (chociaż oczywiście nie zmienia to rozwiązań równania)
Kamil
A co w takim wypadku gdy podczas liczenia jest takie dzielenie przez ujemną? Konkretnie chodzi mi o zadanie 9 gdzie dochodzi się do momentu (x-1)^2*(x+5) / (x+1)^3
Havret
Właśnie tylko co się dzieje, kiedy „dziedzina pochodnej będzie różna od dziedziny funkcji”?
Krystian Karczyński
Trzeba kombinować 🙂
Zasadniczo dziedzina pochodnej nie może być „szersza” od dziedziny funkcji, bo pochodną liczymy tylko tam, gdzie istnieje funkcja (ściślej: nie może być tak, że dziedzina pochodnej NIE zawiera się w dziedzinie funkcji). Jeśli więc dziedzina pochodnej wyjdzie pozornie „szersza” (na przykład funkcja y=lnx i jej pochodna), trzeba ją „zawęzić” (ściślej: wziąść część wspólną dziedziny pochodnej i jej funkcji). Wiedząc o tym, odpada nam połowa kłopotów.
Pozostają jeszcze sytuacje takie jak na przykład w funkcji [pmath]y=root{3}{x^2}[/pmath], w których pochodna ma „dziurę” w punkcie 0, a funkcja jej nie ma. Wtedy trzeba pamiętać, że warunkiem istnienia ekstremum jest tylko zmiana monotoniczności funkcji, a nie jakieś istnienie pochodnej. Jeśli funkcja zmienia monotoniczność w zerze, tzn. jeśli na lewo od zera pochodna ma inny znak niż na prawo od zera (a tak jest w naszym przykładzie), to funkcja MA tam ekstremum, mimo, że w tym punkcie pochodna nie istnieje. Na wykresie ekstremum to wygląda jak „ostrze”.
Matylda
a co z warunkiem koniecznym na istnienie ekstremum ? przeciez pochodna funkcji musi byc rowna 0 aby istanialo ekstremum funkcji. prosze o szybka odpowiedz
Krystian Karczyński
To prawda, takie jest warunek konieczny istnienia ekstremum, ale tylko funkcji RÓŻNICZKOWALNYCH w danym punkcie, a nie w ogóle wszystkich.
Jeżeli funkcja nie jest w ogóle różniczkowalna w danym punkcie, nie dotyczy się jej ten warunek.