Pochodne funkcji i zadania optymalizacyjne [REMASTERED]
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Zadania optymalizacyjne
Zadania optymalizacyjne to takie zadania, w których trzeba znaleźć takie wartości parametrów, dla których wartość od nich zależna jest maksymalna (albo minimalna).
Do takich zadań świetnie nadają się pochodne funkcji.
Przykład na zadanie optymalizacyjne z wykorzystaniem pochodnych funkcji
Chcemy wykonać ogrodzenie na wybieg dla naszego pieska Azorka. Mamy 40 metrów siatki na płot, chcemy, żeby wybieg miał kształt prostokąta i jednym bokiem przylegał do stodoły.
Jakie powinny być wymiary wybiegu, żeby Azor miał jak najwięcej miejsca (powierzchni)? I gdzie w tym miejsce na pochodne funkcji?
Jeżeli ogrodzimy teren dla Azora w ten sposób:
…mamy 40 metrów siatki na płot wykorzystane, ale Azorek ma tylko (pole wybiegu – pole prostokąta):
do biegania, szczekania i kopania rowów.
Jeżeli ogrodzimy inaczej:
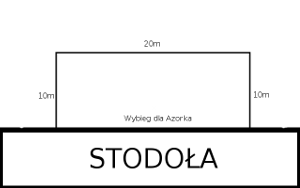
Druta wykorzystaliśmy tyle samo, ale Azorek jest bardziej radosny, bo ma aż (pole wybiegu = pole prostokąta):
do dyspozycji (czyli prawie 3 razy więcej, niż za pierwszym ułożeniem).
Pochodne funkcji już czekają na nas za zakrętem, bo jest to typowe zadanie optymalizacyjne.
Jak należało by ustalić wymiary wybiegu, aby zmaksymalizować jego powierzchnię?
Jeśli oznaczymy boki prostokąta zmiennymi:
Jasne jest, że spełnione musi być równanie: 
.
Dążymy do tego, żeby pole prostokąta było maksymalne, więc: 
.
Z pierwszego równania wyznaczamy 
, podstawiamy do wyrażenia, które chcemy zmaksymalizować i mamy: 
, a po przemnożeniu: 
.
Jest to funkcja kwadratowa i aby wyznaczyć jej maksimum możemy użyć pochodnej: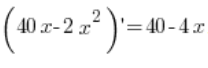 
.
Aby obliczyć ekstremum lokalne funkcji wyliczoną pochodną przyrównujemy do zera:
obliczamy 
:
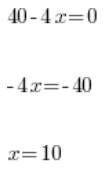
… i mamy wartość , dla której wybieg ma maksymalny rozmiar. Azorek najbardziej więc będzie szczęśliwy z wybiegu o wymiarach 10 metrów na 20 metrów na 10 metrów (tak jak na drugim rysunku).
Zadanie oczywiście można było rozwiązać obliczając wierzchołek funkcji kwadratowej, ale czy nie prościej było jednak pochodnymi? 
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Wow , to nie takie trudne jak myślałem . Dzięki wielkie 🙂
haha xd
Teraz już rozumiem, dzięki. Właściwie to tak samo się liczy rozkładanie liczby na 2 składniki.