Największy problem z zadaniami na macierze…
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Macierze jest to temat stosunkowo prosty. Schematy rozwiązywania zadań są nieskomplikowane i nie wymagają wielkiej wiedzy, starczy ta z gimnazjum, czy może nawet podstawówki.
Wiąże się jednak z nimi jeden kłopot – żeby policzyć głupi rząd macierzy, czy wyznacznik nawet niskiego stopnia trzeba wykonać naprawdę dużo operacji matematycznych.
Błędy rachunkowe w liczeniu zadań
Prostych – typu dodawanie i mnożenie liczb dodatnich i ujemnych, ale jest ich sporo do wykonania – może kilkadziesiąt, a może kilkuset. Łatwo więc o błąd rachunkowy typu jakieś głupie 
, a jeden taki błądzik rozkłada całe zadanie.
Każdy ma swój współczynnik prostych błędów rachunkowych i na setkę prościutkich operacji ileś tam razy się myli. To nic niezwykłego i to nie mija z wiekiem. “Głupie błędy” towarzyszyć nam będą zawsze. Ten współczynnik można i należy jednak obniżać.
Rozwiązanie
Jeden sposób to rozwiązywanie dużej ilości zadań z macierzy (to naprawdę pomaga), a drugi – rozpisywanie wszystkich obliczań maczkiem na marginesie albo w brudnopisie.
Mnożąc macierze rozpisuj. Dodając wiersze przy liczeniu wyznacznika macierzy rozpisuj. Nie próbuj rachować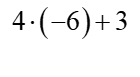 
w pamięci. Zobaczysz, że Twoja pamięć wzrokowa to Twój najlepszy przyjaciel.
Powodzenia w rachowaniu macierzy!
Pomoże Ci w tym także z pewnością mój Kurs im dedykowanym – Kurs Macierze 🙂
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Witam jeśli mam mnożenie macierzy przez liczbę i przed liczbą stoi “-” np. Macierz -2*Macierz to czy mnożę to macierz przez -2 czy 2. I dlaczego? Pozdrawiam
Hej! Jeśli wszystko przemnożysz przez (-2), to wtedy otrzymasz DODAWANIE dwóch macierzy, bo ten minus jakby wciągasz do środka drugiej macierzy.
Na przykładzie zwykłego wyrażenia:
(x+2y) -2*(2x-7y) = (x+2y) + (-4x+14y)
Jeśli pomnożysz tylko razy (2), to minus zostanie na zewnątrz, będziesz miał ODEJMOWANIE dwóch macierzy 🙂
Ten sam przykład:
(x+2y) -2*(2x-7y) = (x+2y) – (4x-14y)
Witam. Czy mógłby ktoś wytłumaczyć mi te zagadnienia i przedstawić krok po kroku rozwiązania tych zadań? Takie zadania będę miał na kolokwium we wtorek, a nie potrafię tego zbytnio ogarnąć z książek i nie ma tego w kursach1. Wyznacz bazę i wymiar powłoki liniowej następujaącego układu wektorówa1 = [1,0,0,¡1] a2 = [2,1,1,0] a3 = [1,1,1,1] a4 = [1,2,3,4] a5 = [0,1,2,3]2. Znajdź współrzędne wektora w podanej bazieB = \{ [1,2,3],[3,2,-5],[1,-1,1] }v = [6,2,-7]3. Dany jest układ wektorów w przestrzeni R4x1 = [2,1,3,-1]x2 = [-1,1,-3,1]x3 = [4,5,3,-1]x4 = [1,5,-3,1]Określ wymiar podprzestrzeni (powłoki liniowej) rozpietej przez te wektory.Wybierz baz˛e, wyznacz wspłłrz˛edne wektorów niebazowych w wybranej bazie,sprawdź, czy x = [6,-3,15,-5] należy do tej podprzestrzeni. Jeśli tak, towyznacz jego współrzędne w wybranej bazie. Wybierz inna˛ baze˛, wyznacz macierzprzejścia z bazy do bazy oraz macierz odwrotna˛, wyznacz współrzędnewszystkich wektorów w nowej bazie.
witam, czy gdy potęguje macierz to jak wtedy zmienia sie wyznacznik? muszę podnieść daną macierz do danej potęgi i z tego policzyc wyznacznik czy jest jakas szybsza metoda?
Witam. Jak zrobić poniższe zadanie? “Zbadać dla jakich wartości parametrów a i b rozwiązanie układu równań3x – 2y +z=b5x -8y +9z=32x +y +az= -1jest zbiorem a)jednoelemen\towym b)nieskończonym c)pustym.” Z góry dzięki za pomoc ! 😀
Rozwiązanie tego zadania może Pan podejrzeć tutaj 🙂
Witam, jak policzyć macierz A do potęgi 424? Elementy macierzy A to: A11=1, A12=-1, A21=-1, A22=2.
Dzień dobry,
Chciałbym poznać schemat rozwiązywania zadań z równaniami macierzowymi tego typu:
np. (AX + B)T = C
gdzie: A, B i C to podane macierze, X jest macierzą szukaną, a T – transponowanie
\displaystyle {{\left( {AX+B} \right)}^{T}}=C
Wiem, że \displaystyle {{A}^{T}}=B\Leftrightarrow A={{B}^{T}}
Stąd
\displaystyle \begin{matrix}AX+B={{C}^{T}} \\ AX={{C}^{T}}-B\mathop{{}}_{{}}/{{\cdot }_{L}}{{A}^{{-1}}} \\ X={{A}^{{-1}}}\left( {{{C}^{T}}-B} \right)\end{matrix}
Witam,
Mam problem z tym przykładem jest jakiś wzór czy po prostu podnieść każdą do 3 potęgi, tu wynik byłby taki sam, a na innych liczbach będzie działało tak samo ?:)
|1 0 1|^3
|0 1 0|
|1 0 1|
Konkretnego wzoru chyba nie ma by podnieść jakąś macierz do trzeciej potęgi, zwłaszcza gdy elementami macierzy są różne liczby.
Wyjątkiem są macierze z jedynkami (tak jak tutaj), czasami przez podniesienie do kwadratu czy nawet trzeciej potęgi można by “znaleźć” wzór na macierz^n
Ale wracając do Pani pytania, WAŻNE – podnoszenie macierzy do potęgi NIE oznacza podnoszenia każdego jej elementu do tej potęgi 😉 Czyli tutaj wynik nie będzie taki sam, jeśli dobrze Panią rozumiem 😉
W tym przypadku trzeba krokami, to znaczy najpierw przeliczyć macierz A do kwadratu, czyli \displaystyle {{A}^{2}}=A\cdot A
Następnie wynik znów pomnożyć razy ta sama macierz bo
\displaystyle {{A}^{3}}=A\cdot A\cdot A={{A}^{2}}\cdot A
a jezeli mam macierz do potegi 12 czy musze ja przemnozyc 12 razy czy jest na to jakas szybsza metoda? {1 -2}
{1-3}
z gory dziekuje za pomoc
Witam serdecznie , zauważyłem podobny przykład na górze do mojego , chciałbym się spytać jakby odpowiedź wyglądała w moim przypadku.
x+py-z =1
x+10y-6z=p
2x-y+pz=0
Dla jakiego p mamy dokładnie jedno rozwiązanie i dla jakiego p mamy więcej niż jedno rozwiązanie ?
Witam.
Liczymy wyznacznik główny:
W=\left| \begin{matrix}
1 & p & -1 \\
1 & 10 & -6 \\
2 & -1 & p \end{matrix} \right|=10p+1-12p+20-6-{{p}^{2}}=-{{p}^{2}}-2p+15
Sprawdzamy, kiedy równy jest 0:
-{{p}^{2}}-2p+15=0
\Delta ={{\left( -2 \right)}^{2}}-4\cdot \left( -1 \right)\cdot 15=64
{{p}_{1}}=\frac{-\left( -2 \right)-8}{2\cdot \left( -1 \right)}=3
{{p}_{2}}=\frac{-\left( -2 \right)+8}{2\cdot \left( -1 \right)}=-5
Czyli układ ma dokładnie 1 rozwiązanie dla p\ne 3i p\ne -5.
Teraz sprawdzam przypadek, gdy p=3:
{{W}_{x}}=\left| \begin{matrix}
1 & 3 & -1 \\
3 & 10 & -6 \\
0 & -1 & 3 \end{matrix} \right| =30+3-6-27=0
{{W}_{y}}=\left| \begin{matrix}
1 & 1 & -1 \\
1 & 3 & -6 \\
2 & 0 & 3 \end{matrix} \right| =9-12+6-3=0
{{W}_{z}}=\left| \begin{matrix}
1 & 3 & 1 \\
1 & 10 & 3 \\
2 & -1 & 0 \end{matrix} \right| =-1+18-20+3=0
Wszystkie wyznaczniki wyszły równe 0, zatem układ ma więcej niż 1 rozwiązanie (a konkretnie nieskończenie wiele rozwiązań) dla p=3.
Sprawdzam jeszcze przypadek dla p=-5:
{{W}_{x}}=\left| \begin{matrix}
1 & -5 & -1 \\
-5 & 10 & -6 \\
0 & -1 & -5 \end{matrix} \right|=-50-5-6+125\ne 0
Zatem w tym przypadku układ nie ma rozwiązań.
x+y+az=1
x-ay+z=11
x-y+z=a
jak rozwiązac macierz tego typu gdy wystepuje oddatkowa niewiadoma a??
No własnie o to chodzi, że ato NIE jest dodatkowa niewiadoma. ato jest tzw. parametr. Dla różnych wartości tego parametru mamy różne rozwiązania x, y,z.
Ten układ możemy atakować od razu wzorami Cramera, ma ma tyle samo równań co niewiadomych. Liczę wyznacznik główny:
W=\left| \begin{matrix}
1 & 1 & a \\
1 & -a & 1 \\
1 & -1 & 1 \end{matrix} \right|=-a-a+1+{{a}^{2}}+1-1= {{a}^{2}}-2a+1
… i przyrównuję go do zera, żeby sprawdzić, dla jakich wartości parametru abędę miał jedno rozwiązanie:
{{a}^{2}}-2a+1=0
\Delta ={{\left( -2 \right)}^{2}}-4\cdot 1\cdot 1=0
{{a}_{1,2}}=\frac{-\left( -2 \right)}{2\cdot 1}=1
Zatem dla a=1wyznacznik główny układu jest równy 0, czyli dla a\ne 1mogę liczyć rozwiązania (tak jak to się po prostu robi wzorami Cramera):
{{W}_{x}}=\left| \begin{matrix}
1 & 1 & a \\
11 & -a & 1 \\
a & -1 & 1 \end{matrix} \right|= -a-11a+a+{{a}^{3}}+1-11 ={{a}^{3}}-11a-10
x=\frac{{{a}^{3}}-11a-10}{{{a}^{2}}-2a+1}
{{W}_{y}}=\left| \begin{matrix}
1 & 1 & a \\
1 & 11 & 1 \\
1 & a & 1 \end{matrix} \right|= 11+{{a}^{2}}+1-11a-a-1 ={{a}^{2}}-12a+11
y=\frac{{{a}^{2}}-12a+11}{{{a}^{2}}-2a+1}
{{W}_{z}}=\left| \begin{matrix}
1 & 1 & 1 \\
1 & -a & 11 \\
1 & -1 & a \end{matrix} \right|= -{{a}^{2}}-1+11+a+11-a=-{{a}^{2}}+21
z=\frac{-{{a}^{2}}+21}{{{a}^{2}}-2a+1}
Natomiast w przypadku, gdy a=1i wyznacznik główny jest równy 0liczę tylko (korzystając z poprzedniego rozpisania):
{{W}_{x}}={{1}^{3}}-11\cdot 1-10\ne 0i stąd wniosek, że dla takie (i tylko takiej) wartości parametru aukład jest sprzeczny.
Dzień dobry, moje pytanie brzmi następująco: które rozwiązania w macierzach nazywamy bazowymi, ogólnymi a które szczegółowymi? Czym się różnią? Mam jutro kolokwium i bardzo prosiłabym o pomoc.
Witam, we wtorek przede mną egzamin z algebry liniowej.
Mam problem z takim zadaniem.
Oblicz A^2009
gdzie A = {{3/5,4/5},{4/5,-3/5}}
Jak to rozwiązać najszybciej?
WolframAlpha podaje nam ciekawy wynik:
={{3/5,4/5},{4/5,-3/5}}^2009
Teraz już tylko dojść do niego 🙂
Niech Pani podniesie tą macierz do kwadratu i zauważy, że:
{{\left[ \begin{matrix}
\frac{3}{5} & \frac{4}{5} \\
\frac{4}{5} & -\frac{3}{5} \end{matrix} \right]}^{2}}=\left[ \begin{matrix}
\frac{3}{5} & \frac{4}{5} \\
\frac{4}{5} & -\frac{3}{5} \end{matrix} \right]\cdot \left[ \begin{matrix}
\frac{3}{5} & \frac{4}{5} \\
\frac{4}{5} & -\frac{3}{5} \end{matrix} \right]=\left[ \begin{matrix}
1 & 0 \\
0 & 1 \end{matrix} \right]=I
Czyli macierz Apodniesiona do kwadratu daje macierz jednostkową I
{{A}^{2}}=I
Czyli można przekształcić:
{{A}^{2009}}={{A}^{2008}}\cdot A={{\left( {{A}^{2}} \right)}^{1004}}\cdot A={{I}^{1004}}\cdot A
Macierz jednostkowa razy macierz jednostkowa daje oczywiście zawsze macierz jednostkową, ma Pani więc:
{{I}^{1004}}\cdot A=I\cdot A=A=\left[ \begin{matrix}
\frac{3}{5} & \frac{4}{5} \\
\frac{4}{5} & -\frac{3}{5} \end{matrix} \right]
Czyli w przypadku tej macierzy:
{{\left[ \begin{matrix}
\frac{3}{5} & \frac{4}{5} \\
\frac{4}{5} & -\frac{3}{5} \end{matrix} \right]}^{2009}}=\left[ \begin{matrix}
\frac{3}{5} & \frac{4}{5} \\
\frac{4}{5} & -\frac{3}{5} \end{matrix} \right]
własnie wychodziło mi t=0,4 ale nie wiedziałem co z tym dalej zrobic 🙂 wielkie dzięki:)
witam.Mam prosbe ogromną , jak roziwiązac układ równan
x-y=0
2x+y=1
x-3y=-1
Rozwiązuje to metodą operacji elementarnych i nie wiem gdzie robie błąd i wychodzi mi ze x=1/3 i y=1/3.Czy układ bedzie sprzeczny ? bo w 3 linijce wychodzi mi 0=-1/3.Bardzo proszę o pomoc.I jeszcze jendo działanie:
2x-y+t=1
4x-2y-3t=0
Witam, tak ten pierwszy układ jest sprzeczny. Jeżeli x=1/3, y=1/3 to ma być “wynik” to nie jest to prawidłowy wynik, bo ten układ jest sprzeczny i nie ma rozwiązań.
Ten drugi dla odmiany to układ nieoznaczony, ma nieskończenie wiele rozwiązań. Po przemnożeniu pierwszego równania przez -2 i dodaniu do drugiego wyjdziemy na t=\frac{2}{5}, możemy np. za y przyjąć parametr {\alpha}, wstawić do któregoś równań i wyznaczyć x.
Obejdzie się bez macierzy nawet 🙂