Postać trygonometryczna liczby zespolonej – różne kąty, to samo rozwiązanie?
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Funkcje trygonometryczne (wykorzystywane w postaci trygonometrycznej liczby zespolonej) są 
-okresowe, co oznacza, że dla dowolnych argumentów różniących się o np. 
przyjmują tą samą wartość.
Na przykład:
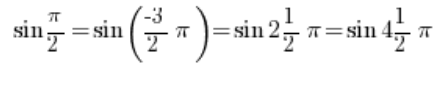
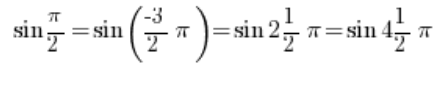
Tak więc na przykład liczba zespolona w postaci trygonometrycznej:
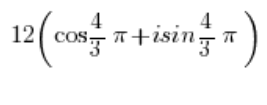
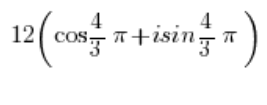
to taka sama liczba zespolona jak:
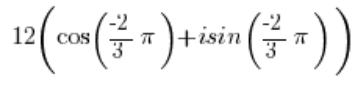
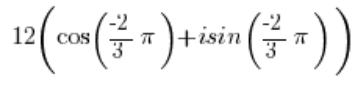
bo argumentu funkcji trygonometrycznych różnią się o .
Jakich argumentów używać?
Jakich argumentów przyjęło się więc używać? W Polsce z przedziału 
. W starszych jednak podręcznikach, lub cudzoziemskich mogą to być na przykład argumenty z przedziału 
. Warto mieć to na uwadze, sprawdzając poprawność swoich wyliczeń z liczb zespolonych z odpowiedziami z podręcznika.
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
ok. przespałam się z tym i już wiem na czym polegał mój błąd… tylko…mi wychodzi minus przed cos i sin… i wydaje mi się że tak powinno być.
odp podana przez wykładowcę jest chyba nie do końca dobra….
Mój problem jest następujący (nie wiedziałam jak inaczej go zwerbalizować dlatego umieściłam na stronie… i nie mogłam znaleźć opcji nowy wątek czy coś temu pochodnego…;pp):
chcę jeszcze dodać to co nam na lekcji mówił pan, że moduły się mnoży a kąty dodaje…
hmm…ale nie wiem czemu jak robię zadania Pana sposobem to wychodzą mi inne wyniki:(
np w z1 koledze wyszedł minus przed cosinusem…
w sensie jak jest liczone fi np. fi=pi – pi/6 to Pana sposobem wyjdzie nam fi=5/6pi i to fi podstawiamy do cosinusa i sinusa…
natomiast kolega podstawia: pi-\pi/6 do cosinusa i sinusa i rozpatruje to jako ze w 2iej ćwiartce cos jest ujemny wiec minus przed cos, a sin jest dodatni wiec znak zostaje…
hmm? pewnie ja gdzieś błąd zrobiłam…. ale nie umiem go znaleźć…