किसी फ़ंक्शन की चरम सीमा के अस्तित्व की पर्याप्त शर्त

फंक्शन की एक्सट्रीमा व्याख्यान 7

विषय: फंक्शन की एक्सट्रीमा के अस्तित्व की पर्याप्त शर्त (डेरिवेटिव के चिन्ह में परिवर्तन)।

सारांश

जैसा कि पिछले व्याख्यान में पाया गया, केवल यह कि एक बिंदु पर फंक्शन का डेरिवेटिव शून्य के बराबर है, यह आवश्यक नहीं है कि स्वयं फंक्शन उस बिंदु पर एक्सट्रीमा प्राप्त करता है। यहाँ हम बताएंगे कि कौन सी शर्तें पर्याप्त हैं, ताकि फंक्शन किसी बिंदु पर एक्सट्रीमा प्राप्त कर सके।

एक्सट्रीमा के अस्तित्व की पर्याप्त शर्तें

मान लीजिए कि $x_0$ बिंदु के किसी परिवेश में फंक्शन $f \left(x \right)$ का एक सीमित डेरिवेटिव $f' \left( x \right)$ है:

यदि इस परिवेश में $x_0$ के बाएँ ओर डेरिवेटिव के मान सकारात्मक हैं, और $x_0$ के दाएँ ओर नकारात्मक हैं – तो फंक्शन $x_0$ बिंदु पर अधिकतम मान लेता है
यदि इस परिवेश में $x_0$ के बाएँ ओर डेरिवेटिव के मान नकारात्मक हैं, और $x_0$ के दाएँ ओर सकारात्मक हैं – तो फंक्शन $x_0$ बिंदु पर न्यूनतम मान लेता है

वास्तव में, पिछले व्याख्यान में प्रस्तुत फंक्शन की मोनोटोनिसिटी के लेमा के अनुसार, यदि फंक्शन का ड ेरिवेटिव सकारात्मक मान लेता है, इसका मतलब है कि फंक्शन बढ़ रहा है। यदि डेरिवेटिव नकारात्मक मान लेता है, इसका मतलब है कि फंक्शन घट रहा है।

इसलिए, यदि डेरिवेटिव “अपना चिन्ह बदलता है”, तो यह भी फंक्शन की मोनोटोनिसिटी में परिवर्तन को दर्शाता है, उदाहरण के लिए मामला 1:

बाएं से का डेरिवेटिव सकारात्मक है, और दाएं से नकारात्मक। इसका मतलब है कि फंक्शन के बाएं से बढ़ रहा है, और दाएं से घट रहा है। इसलिए इसे कुछ इस तरह दिखना चाहिए: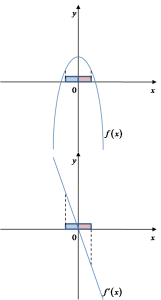
ऊपर दिए गए ग्राफ में हमारे पास फंक्शन (ऊपर) और इसके डेरिवेटिव का ग्राफ है। यह दिखाई देता है कि के ‘बाएं’ वातावरण में (नीले रंग में चिह्नित) डेरिवेटिव सकारात्मक मूल्य लेता है, और फंक्शन बढ़ रहा है। ‘दाएं’ वातावरण में (लाल रंग में चिह्नित) डेरिवेटिव नकारात्मक मूल्य लेता है, और फंक्शन घट रहा है।