समरूप रैखिक समीकरणों की प्रणाली वे प्रणालियाँ हैं जिनमें सभी स्वतंत्र पद 0 के बराबर होते हैं। ये इस प्रकार दिखते हैं:
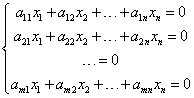
उदाहरण के लिए:
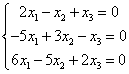
रैखिक समीकरण प्रणालियों में संभावित समाधान की संख्या
याद रखें कि प्रत्येक रैखिक समीकरण प्रणाली में तीन संभावित स्थितियाँ होती हैं:
- प्रणाली में 1 समाधान होता है (जब मुख्य मैट्रिक्स की रैंक = पूरक मैट्रिक्स की रैंक = प्रणाली में अज्ञातों की संख्या:
) - प्रणाली में अनंत समाधान होते हैं (जब मुख्य मैट्रिक्स की रैंक = पूरक मैट्रिक्स की रैंक होती है और अज्ञातों की संख्या से कम होती है )
- प्रणाली में कोई समाधान नहीं होता (जब मुख्य मैट्रिक्स की रैंक पूरक मैट्रिक्स की रैंक के बराबर नहीं होती)
पूरक मैट्रिक्स मुख्य मैट्रिक्स होती है जिसमें स्वतंत्र पदों का एक कॉलम जोड़ा जाता है। समरूप प्रणाली के मामले में, यह एक शून्य का कॉलम होगा। रैंकों की गणना के दौरान इसे आसानी से हटाया जा सकता है और इस प्रकार केवल मुख्य मैट्रिक्स प्राप्त की जा सकती है।
हमारे उदाहरण में, मुख्य मैट्रिक्स की रैंक होती है:
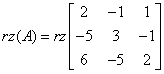
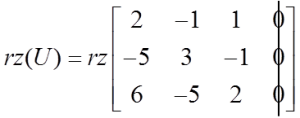
उदाहरण में, हम देख सकते हैं कि 
और हम देख सकते हैं कि यह हमेशा ऐसा होगा, प्रत्येक समरूप प्रणाली में।
समरूप रैखिक समीकरण प्रणाली में संभावित समाधान की संख्या
इस प्रकार, समरूप समीकरण प्रणालियों में केवल स्थितियाँ 1 या 2 ही होंगी। प्रणाली में हमेशा समाधान होंगे, केवल प्रश्न यह है कि यह 1 समाधान होगा या अनंत समाधान होंगे।
आगे बढ़ते हैं।
हम कुछ ऐसा परिभाषित करें जिसे “शून्य समाधान” कहा जाता है। शून्य समाधान वह समाधान होता है जिसमें सभी अज्ञातों के मान शून्य होते हैं।
समरूप समीकरण प्रणालियों के बारे में बात करते समय, यह देखा जा सकता है कि:
शून्य समाधान हमेशा समरूप प्रणाली का समाधान होता है।
यह जांचना आसान है: यदि सभी अज्ञातों को समीकरणों में शून्य मान लिया जाए, तो यह स्पष्ट रूप से देखा जा सकता है कि प्रत्येक समरूप प्रणाली का प्रत्येक समीकरण हमेशा संतुष्ट होगा।
इस प्रकार, यदि हम जानते हैं कि समरूप रैखिक समीकरण प्रणाली में 1 समाधान है (जब 
), तो हम यह भी जानते हैं कि यह निश्चित रूप से शून्य समाधान है।
यदि हम जानते हैं कि समरूप रैखिक समीकरण प्रणाली में अनंत समाधान हैं (जब 
), तो हम जानते हैं कि प्रणाली में शून्य समाधान है, लेकिनसाथ ही कुछ गैर-शून्य समाधान भी हैं।
यदि प्रश्न में कहा जाए: “जांचें कि समरूप प्रणाली में गैर-शून्य समाधान हैं या नहीं”, तो केवल यह दिखाना पर्याप्त है कि यह एक अनिश्चित प्रणाली है, जिसमें मुख्य मैट्रिक्स की रैंक और पूरक मैट्रिक्स की रैंक अज्ञातों की संख्या से कम है।
कुछ प्रणालियों में यह बहुत सरल है, उदाहरण के लिए यहाँ:
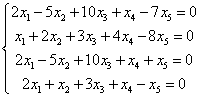
प्रणाली की मुख्य मैट्रिक्स में 4 पंक्तियाँ और 5 स्तंभ होंगे, इसलिए इसकी रैंक अधिकतम 4 होगी। पूरक मैट्रिक्स की रैंक भी 4 होगी – हम पहले ही जानते हैं कि क्यों। अज्ञातों की संख्या 5 है। इसलिए, तुरंत कहा जा सकता है कि प्रणाली अनिश्चित है और इस प्रणाली के कुछ गैर-शून्य समाधान हैं।
