फ़ंक्शन्स के क्षैतिज और तिरछे अभिसारियों के बीच का संबंध यह है कि क्षैतिज अभिसारी तिरछे अभिसारियों का एक विशेष मामला हैं। इसलिए, हर क्षैतिज अभिसारी एक तिरछा अभिसारी है, पर हर तिरछा अभिसारी क्षैतिज नहीं होता है।
आपको फ़ंक्शन के अभिसारियों की गणना को आसान बनाने के लिए इसका उपयोग करना चाहिए। मूल रूप से इस विषय पर दो दृष्टिकोण हैं:
1. सबसे पहले हम क्षैतिज अभिसारियों की गणना करते हैं
यह दृष्टिकोण मेरे वीडियो कोर्स “फ़ंक्शन्स के व्यवहार का अध्ययन” में दिखाया गया है।
एक फ़ंक्शन में क्षैतिज अभिसारी के होने की शर्त है:
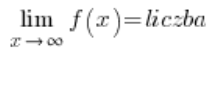 या
या 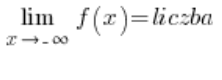
यदि क्षैतिज अभिसारी निकलते हैं, तो हम तिरछे अभिसारियों की गणना नहीं करते (मानो तिरछे पहले ही निकल चुके हों – याद रखें कि क्षैतिज भी एक प्रकार के तिरछे होते हैं)। हालाँकि, यदि क्षैतिज अभिसारी नहीं निकलते हैं तो हमें समस्या होती है – हमें तिरछे अभिसारियों की गणना फिर से करनी पड़ती है।
बेशक, स्थिति थोड़ी और जटिल है: क्षैतिज अभिसारी ![]() में “निकल” सकता है, और
में “निकल” सकता है, और ![]() में “नहीं निकल” सकता है। ऐसी स्थिति में हम
में “नहीं निकल” सकता है। ऐसी स्थिति में हम ![]() में तिरछे अभिसारी की मौजूदगी की जाँच नहीं करेंगे (क्योंकि वह पहले ही वहाँ निकल चुका है), लेकिन हमें
में तिरछे अभिसारी की मौजूदगी की जाँच नहीं करेंगे (क्योंकि वह पहले ही वहाँ निकल चुका है), लेकिन हमें ![]() में इसकी जाँच करनी होगी।
में इसकी जाँच करनी होगी।
2. पहले तिरछे अभिसारी गणना करें
…और फिर क्षैतिज अभिसारी हमें (या नहीं) स्वचालित रूप से मिल जाएंगे; हमें केवल सही तरीके से उत्तरों की व्याख्या करनी होगी। इस पद्धति को मैं अपने कोर्स में नहीं दिखाता हूँ। इसकी कमी यह है कि फ़ंक्शन में तिरछे अभिसारी के होने की शर्तें थोड़ी जटिल होती हैं:
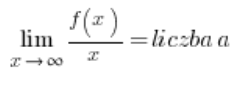 और
और 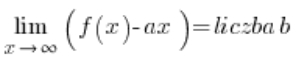
या:
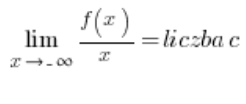 और
और 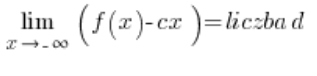
…और इसका लाभ यह है कि एक बार गणना कर लेने के बाद, आगे कुछ भी गणना करने की ज़रूरत नहीं होती। यदि शर्तें पूरी होती हैं और तिरछे अभिसारी के अस्तित्व की शर्तों में से नंबर ![]() (या
(या ![]() ) शून्य के बराबर होता है, तो यह दर्शाता है कि तिरछा अभिसारी वास्तव में एक क्षैतिज अभिसारी है।
) शून्य के बराबर होता है, तो यह दर्शाता है कि तिरछा अभिसारी वास्तव में एक क्षैतिज अभिसारी है।
काम को और भी छोटा करने के लिए, हम सीधे गणना कर सकते हैं:
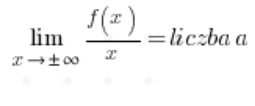 और
और 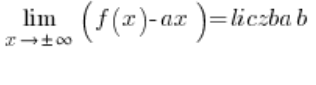
और ![]() और
और ![]() के लिए शर्तों को अलग से गणना करनी चाहिए तभी जब यह आवश्यक हो (जब परिणाम में अंतर आएगा कि क्या x
के लिए शर्तों को अलग से गणना करनी चाहिए तभी जब यह आवश्यक हो (जब परिणाम में अंतर आएगा कि क्या x ![]() की ओर जा रहा है या
की ओर जा रहा है या ![]() की ओर).
की ओर).