यूलर की प्रतिस्थापना – इसकी आवश्यकता किसे है?
अनिश्चित इंटिग्रलों में यूलर की प्रतिस्थापना एक अगला कदम है, जो कि तर्कसंगत इंटिग्रलों, त्रिकोणमितीय इंटिग्रलों और मूल इंटिग्रलों के बाद आता है (या कुछ के अनुसार: “अतर्कसंगत इंटिग्रल”)। इसका मतलब है कि ज्यादातर छात्रों को इससे सामना नहीं करना पड़ेगा, मैंने भी इसे अपने अनिश्चित इंटिग्रलों के कोर्स में नहीं डाला है।
हालांकि, गणितीय विषयों में या सच में, सच में “मजबूत” गणितिक वाले छात्रों का एक बड़ा समूह है, जिन्हें यूलर की प्रतिस्थापना से निपटना होगा और उनके (और उत्सुक लोगों के) लिए मैं आमंत्रित करता हूं। मैं यूलर की सभी तीन प्रकार की प्रतिस्थापनाओं को चर्चा करूंगा (इस पोस्ट में मैं पहले प्रकार पर ध्यान दूंगा) और प्रत्येक के लिए एक उदाहरण दूंगा।
चलो शुरू करते हैं।
किन इंटिग्रलों को हम यूलर की प्रतिस्थापना से हल करते हैं?
यूलर की प्रतिस्थापना से हम इस तरह के इंटिग्रलों को हल करते हैं:
…यानी कुछ ऐसे संबंध जो 
और 
से बनते हैं। इसे हम मूल इंटिग्रलों (“अतर्कसंगत”) के विषय की एक “विस्तार” के रूप में मान सकते हैं।
यूलर की प्रतिस्थापना से हम वे इंटिग्रल हल करते हैं, जिन्हें साधारण तरीके से हल नहीं किया जा सकता, ज़ाहिर है। उदाहरण के लिए, इंटिग्रल:
यह एक है इंटिग्रल, जिसमें हमारे पास और का संबंध है, लेकिन इसे बहुत आसानी से साधारण प्रतिस्थापन: 
से हल किया जा सकता है। इसलिए हम छोटे पक्षी पर तोप से गोली नहीं चलाते और ऐसे सरल इंटिग्रलों में यूलर की प्रतिस्थापना का इस्तेमाल नहीं करते।
लेकिन अब इस इंटिग्रल को देखें:
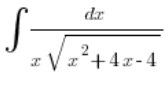
हम देखते हैं कि स्थिति थोड़ी जटिल है, पहले से जानी गई प्रतिस्थापनाएँ 
, या 
(जिनसे हम नहीं निकाल सकते) यहाँ काम नहीं आएंगी।
हमें एक नया हथियार चाहिए।
यूलर की प्रतिस्थापना – प्रथम प्रकार
जब हमारे पास ऐसा इंटिग्रल हो:
जिसमें 
,
हम यह प्रतिस्थापना करते हैं:
, फिर दोनों तरफ को वर्ग में बदलते हैं, और तत्व 
आपस में कट जाते हैं (और यही हमारा उद्देश्य है), फिर हम (क्रम में):
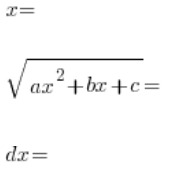
, t के संबंधों के साथ व्यक्त करते हैं, और उसे मूल इंटिग्रल में डालते हैं:
और हमारे पास t का इंटिग्रल है (अगर इसमें कोई x-sy बची हैं, तो हमने गलती की है) और यह एक तर्कसंगत इंटिग्रल है।
ध्यान दें
इसके अलावा, यह जोड़ना भी महत्वपूर्ण है कि व्यवहार में, कई छात्रों को केवल प्रथम प्रकार की यूलर प्रतिस्थापनाएँ सिखाई जाती हैं, और केवल उन इंटिग्रलों के लिए:
, यानी ऐसे, जहाँ मानो 
आइए यूलर की प्रथम प्रकार की प्रतिस्थापना को एक उदाहरण के माध्यम से समझें:
उदाहरण 1
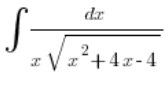
हम पाते हैं कि यह एक ऐसा इंटिग्रल है जिसमें और का संबंध है। इसे साधारण तरीके से हल नहीं किया जा सकता। यहाँ है (जहां 
यहाँ 
का गुणांक है, हमारे उदाहरण में यह 1 है)।
तो हम यूलर की प्रथम प्रकार की प्रतिस्थापना का प्रयोग करेंगे।
मैं प्रतिस्थापित करता हूँ:
यानी सीधे तौर पर:
फिर मैं दोनों तरफ को वर्ग में बदलता हूँ:
के संबं
धित घटक दोनों तरफ कट जाते हैं (और यही हर बार होना चाहिए):
और अब हमें , और 
(इस क्रम में) निर्धारित करना है।
आइए से शुरू करते हैं:
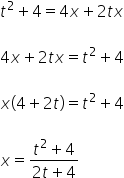
हमारे पास t के रूप में व्यक्त है। अब हम आगे बढ़ते हैं की ओर, जो हमारे उदाहरण में है: 
.
हम वापस जाते हैं अपनी पहली प्रतिस्थापना की ओर, जिसमें था:
अब हमें पता चला है (देखें, क्यों महत्वपूर्ण है क्रम, है ना?), इसलिए हम लिख सकते हैं:
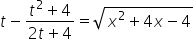
यानी:
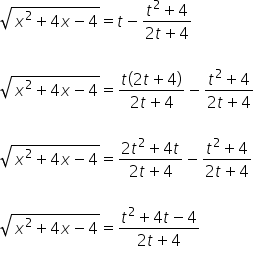
इसलिए हमारे पास t के रूप में व्यक्त है।
अंत में , जिसे हम सीधे निर्धारित की गई के दोनों तरफ विभेदक लेकर प्राप्त करते हैं:
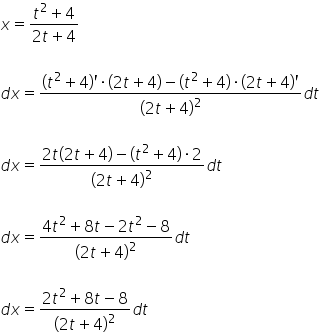
और इस तरह हम को निर्धारित करते हैं। इसलिए हमारे पास है:
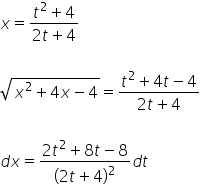
हम इस सब को मूल इंटिग्रल में डालते हैं:
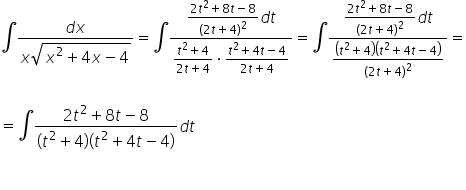
पहली नजर में, यह उबाऊ, थकाने वाला, लेकिन पहले से जाना पहचाना तर्कसंगत इंटिग्रल प्रतीत होता है (सरल भिन्नों में विभाजन, मियानों का दूसरा घटक और अधिक विभाजित हो सकता है)। आम तौर पर यह सही है, लेकिन इस विशेष उदाहरण में हमें थोड़ी किस्मत मिलेगी और 3 पृष्ठों के A4 गणनाओं से गुजरने से हमें बचाया जाएगा:
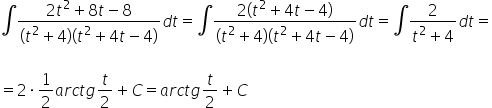
प्रतिस्थापन से वापस कैसे आएं? हमने शुरुआत में क्या किया था:
इससे स्पष्ट है:
तो हमारा परिणाम है:
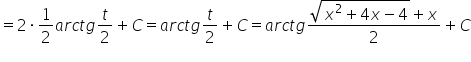
CDN. (अभी भी दो और प्रकार की यूलर प्रतिस्थापनाएँ बाकी हैं, क्या होगा अगर गुणांक शून्य से बड़ा नहीं है?)।
