Condición suficiente para la existencia de un extremo de una función

Extremos de Funciones Lección 7

Tema: Condición suficiente para la existencia de un extremo de función (cambio de signo de la derivada).

Resumen

Como descubrimos en la lección anterior, el hecho de que la derivada de una función en un punto sea igual a 0 no necesariamente significa que la función alcance un extremo en ese punto. Aquí, entonces, discutiremos qué condiciones son suficientes para que una función alcance un extremo en algún punto.

Condiciones suficientes para la existencia de un extremo

Supongamos que en cierto entorno del punto $x_0$ , la función $f \left(x \right)$ tiene una derivada finita $f' \left( x \right)$ :

Si en este entorno de $x_0$ , a la izquierda de $x_0$ , los valores de la derivada de la función son positivos, y a la derecha de $x_0$ son negativos – entonces la función alcanza un máximo en el punto $x_0$
Si en este entorno de $x_0$ , a la izquierda de $x_0$ , los valores de la derivada de la función son negativos, y a la derecha de $x_0$ son positivos – entonces la función alcanza un mínimo en el punto $x_0$

De hecho, de acuerdo con el Lema de Monotonía de Funciones introducido en la lección anterior, si la derivada de la función toma valores positivos, significa que la función está aumentando. Si, por otro lado, la derivada toma valores negativos, significa que la función está disminuyendo.

Por lo tanto, si la derivada „cambia de signo”, esto también indica un cambio en la monotonía de la función , por ejemplo en el caso 1:

La derivada a la izquierda de es positiva, y a la derecha negativa. Esto significa que la función a la izquierda de está aumentando, y a la derecha disminuyendo. Por lo tanto, debe verse algo así: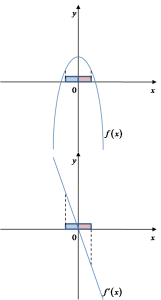
En el gráfico anterior tenemos el gráfico de la función (arriba) y su derivada . Se puede ver que en el „entorno izquierdo” del punto (marcado en azul) la derivada toma valores positivos, y la función está aumentando. En el „entorno derecho” del punto (marcado en rojo) la derivada toma valores negativos, y la función está disminuyendo.