Al resolver problemas con números complejos, es importante recordar que un número complejo en forma trigonométrica se ve así:
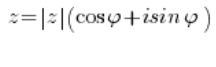
Y solo así. Ni más, ni menos.
Por lo tanto, debes prestar atención a:
¿Cuándo un número complejo está en forma trigonométrica y cuándo no?
- El número:
ESTÁ en forma trigonométrica, donde el módulo del número es igual a 1 (), porque obviamente:
- El número: NO está en forma trigonométrica porque antes de la unidad imaginaria ‘i’ multiplicada por el seno hay un signo negativo, pero debería ser un signo positivo.
Para convertir este número a forma trigonométrica, necesitamos usar fórmulas trigonométricas:
Usando estas fórmulas, podemos convertir:
Las funciones seno y coseno son-periódicas, por lo que su valor es el mismo que . Escribí más sobre este tema en: esta publicación.
Así que al final, tenemos:
…y esto es un número en forma trigonométrica. - El número: NO está en forma trigonométrica porque antes de la unidad imaginaria ‘i’ multiplicada por el seno hay un signo negativo, pero debería ser un signo positivo, y antes del coseno hay un signo negativo, pero debería ser un signo positivo.
Para convertir este número complejo a forma trigonométrica, necesitamos sacar el signo negativo delante del paréntesis:
Convertir el número a forma trigonométrica (esto ya lo sabemos hacer…):
Así que tenemos la multiplicación de dos números en forma trigonométrica:
Para multiplicar números en forma trigonométrica, multiplicamos sus módulos y sumamos sus argumentos (hay una fórmula para esto), así que tenemos:
Y esto es un número en forma trigonométrica. - El número: NO ES un número complejo en forma trigonométrica porque antes del coseno hay un signo negativo, pero debería ser positivo.
Para convertir este número complejo a forma trigonométrica, necesitas sacar el signo negativo frente al paréntesis:
El número -1 debe ser convertido a forma trigonométrica (lo hicimos en el punto 3), de igual manera, el número debe ser convertido a forma trigonométrica (lo hicimos en el punto 2).
Obtenemos:
Usando la fórmula para multiplicar funciones trigonométricas:
Y usando la periodicidad de las funciones seno y coseno:
- El número: NO ES un número complejo en forma trigonométrica porque antes del coseno hay una unidad imaginaria ‘i’ (y no debería estar allí), y antes del seno no hay unidad imaginaria ‘i’.
Necesitas usar las fórmulas trigonométricas conocidas del bachillerato:
Así tenemos:
Y esto ya ES un número complejo en forma trigonométrica. - El número: NO ES un número complejo en forma trigonométrica.
Necesitas intercambiar el seno y el coseno como lo hicimos en el punto 5, y luego resolverlo como en el punto 4. - El número: NO ES un número complejo en forma trigonométrica.
Necesitas intercambiar el seno y el coseno como lo hicimos en el punto 5, y luego resolverlo como en el punto 2. - El número: NO ES un número complejo en forma trigonométrica.
Necesitas intercambiar el seno y el coseno como lo hicimos en el punto 5, y luego resolverlo como en el punto 3.
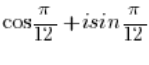ESTÁ en forma trigonométrica, donde el módulo del número es igual a 1 (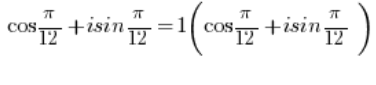
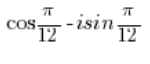), porque obviamente:
NO está en forma trigonométrica porque antes de la unidad imaginaria ‘i’ multiplicada por el seno hay un signo negativo, pero debería ser un signo positivo.
-periódicas, por lo que su valor es el mismo que 
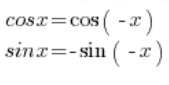
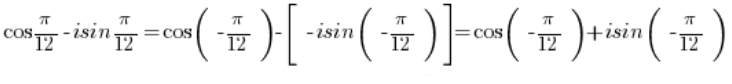
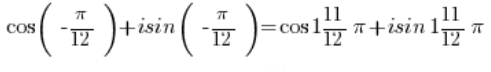
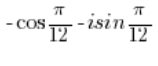NO está en forma trigonométrica porque antes de la unidad imaginaria ‘i’ multiplicada por el seno hay un signo negativo, pero debería ser un signo positivo, y antes del coseno hay un signo negativo, pero debería ser un signo positivo.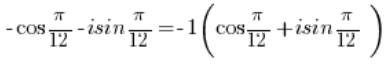
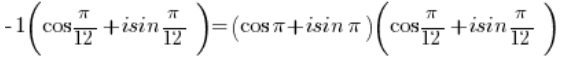
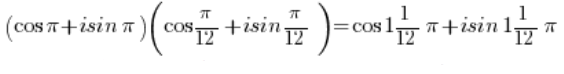
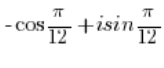a forma trigonométrica (esto ya lo sabemos hacer…):
NO ES un número complejo en forma trigonométrica porque antes del coseno hay un signo negativo, pero debería ser positivo.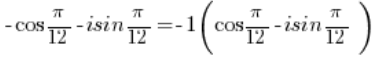
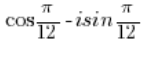debe ser convertido a forma trigonométrica (lo hicimos en el punto 2).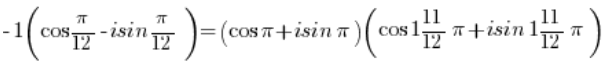
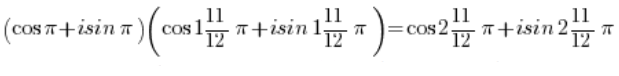
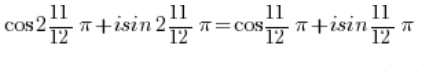
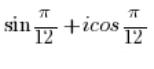NO ES un número complejo en forma trigonométrica porque antes del coseno hay una unidad imaginaria ‘i’ (y no debería estar allí), y antes del seno no hay unidad imaginaria ‘i’.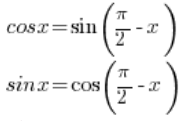
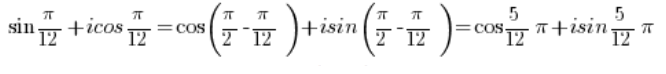
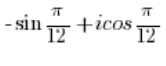NO ES un número complejo en forma trigonométrica.
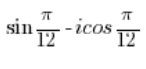NO ES un número complejo en forma trigonométrica.
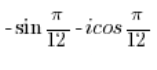NO ES un número complejo en forma trigonométrica.¡Buena suerte! 🙂
