Order of Matrices Lecture 2
Topic: Checking whether vectors form a basis in a linear space
Summary
In this article, I’ll show you how to use the rank of a matrix to check whether vectors form a basis of a linear space.
When do vectors form a basis in linear space?
We call several vectors a basis of a linear space when two conditions are met:
- These vectors are linearly independent (this is where the order of the matrix is used)
- Any other vector in the same space can be represented as a linear combination of these vectors
So to check if several vectors form a basis, you have to show that they satisfy these two conditions.
Calculation of linear independence of vectors
Here the matter is simple. Vectors are arranged by rows (or columns) in a matrix. We count the row of the matrix. The order of a matrix is the maximum number of independent vectors that compose it. So if the rank of a matrix is equal to the number of vectors in it, then they are linearly independent. If it does not come out equal – they are linearly dependent (and do not form a basis in a given space).
Proving that every vector can be expressed as a linear combination of linearly independent vectors
Here we take some arbitrary vector in a given space and show that there are (or not) constants that multiplied by the base vectors added together will be equal to this arbitrary vector. How this is done – I will show further in the example.
Example (task)
For example, we can do the following task:
Excercise 1
Check that the vectors: \vec{x_1} =[1,0,3], \vec{x_2}=[0,2,2], \vec{x_3} =[1,-2,0] form a basis in linear space {\R}^{3}, and if so, represent the vector \vec{a}=[10,2,4] as their linear combination.
We start by checking the linear independence of these vectors. We put them in a matrix and count its rank :
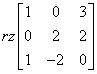We count, count, count (how to do it exactly is shown, for example, in my Matrix Course) and we have the result:
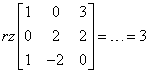If the rank of the matrix is 3, and the vectors are also three, then they are linearly independent . The first condition for the vectors to form a basis in a linear space {\R}^3 is fulfilled.
In the second condition we have to show that any vector belonging to the space {\R}^3 (i.e. three-dimensional) can be represented as the sum of vectors forming – supposedly – a base multiplied by constants. You can write this condition as:
{\forall}_{\vec{x}}{\exists}_{{\alpha_1},{\alpha_2},{\alpha_3}}\vec{x}={\alpha_1}\vec{x_1}+{\alpha_2}\vec{x_2}+{\alpha_3}\vec{x_3}Switching to the notation with coordinates of vectors and their column form (more convenient), this condition will look like this:
Multiplying by constants we get:
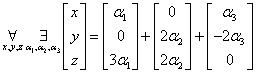And after adding the matrices on the right:
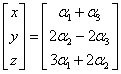The above equation will give us a system of equations:
Note that this system ALWAYS has a solution, no matter how much x,y,z are equal, because the main determinant of the system (from Cramer’s formulas) is different from zero:
So for any x,y,z there will be one {\alpha_1} ,{\alpha_2} ,{\alpha_3} that the system will have a solution. So any vector in a linear space {\R}^3 can be represented as a linear combination of vectors \vec{x_1} ,\vec{x_2} ,\vec{x_3}.
So we have the answer. Vectors \vec{x_1} ,\vec{x_2} ,\vec{x_3} form a basis in linear space {\R}^3.
Let’s recall the command:
Check that the vectors: \vec{x_1} =[1,0,3], \vec{x_2}=[0,2,2], \vec{x_3}=[1,-2,0] form a basis in linear space {\R}^3, and if so, represent the vector \vec{a}=[10,2,4] as their linear combination.
So our mission is not over yet, we still need a vector \vec{a} =[10,2,4] represent as a linear combination of vectors \vec{x_1} =[1,0,3], \vec{x_2} =[0,2,2], \vec{x_3} =[1,-2,0] that is, find such a constant \alpha_1, \alpha_2, \alpha_3, That:
After multiplying by vector constants on the right:
After adding the vectors on the right:
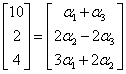What can be written as a system of equations:
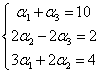We solve this system – for example – by Cramer’s formulas and we get the result:
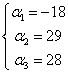So our vector represented as a linear combination of three vectors can be written as:
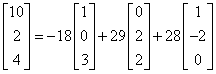And this is our answer.
Let’s do an example where the vectors will NOT be linearly independent, as shown by the order of the matrix.
Exercise 2
Check that the vectors: \vec{x_1} =[4,-1,4], \vec{x_2} =[3,2,5], \vec{x_3} =[8,-2,8] form a basis in linear space {\R}^3.
To check the linear independence of the vectors, we calculate the rank of the appropriate matrix:
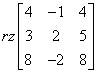We count, count, count and we have the result: 2. So only 2 of these 3 are linearly independent. So these 3 vectors as a whole are not linearly independent. Thus, they do not form the basis of space {\R}^3 . Case closed, we can write a nice, finish answer.
Click to remember what the rank of a matrix is (previous Lecture)< —