How to correctly multiply and divide inequalities

In this post, I will continue with topics from high school that you may not have placed much emphasis on, but which will make your life much easier when you go to college.

This is part 5 – if you just came here now, you can take a look at the previous 4 posts 🙂

Here I will deal with both-side multiplication and division of inequalities.

Dividing inequality? I think I know what this is about…

Yeah. We all already know (although sometimes we forget) about changing the sign of an inequality when multiplying/dividing it by a negative number.

For example:

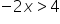$negative 2 x greater than 4$ /:(-2)

$x less than negative 2$ (the inequality sign has changed because I divided both sides by a negative number)

Or:

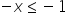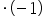
$negative x less or equal than negative 1$ / $times open parentheses negative 1 close parentheses$

$x greater or equal than 1$ (the inequality sign changed after multiplying both sides by a negative number)

But what about multiplying and dividing not by a NUMBER, but by a VARIABLE, for example:

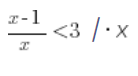
Can we do this multiplication and get:

…?

The correct answer is: NO, WE CAN’T.

We remember the rule: “If we multiply by a positive, we do not change the sign, if we multiply by a negative, we change it.” By multiplying by a variable WE DON’T KNOW whether we are multiplying by a positive or negative number. Variable it can be equal to -100 , and it can also be equal to 15 . The fact that there is no minus sign in front of it does not change anything (it can be negative anyway).

If we don’t know this, we can’t move on…

…because we could only achieve such an inequality if we multiplied by a positive number (without changing the sign), and we DON’T KNOW that.

The same principle applies to division, so we cannot do something like this:

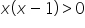$x open parentheses x minus 1 close parentheses greater than 0$ /:x

$x minus 1 greater than 0$

…because, let’s repeat: we don’t know whether x is a positive or negative number.

So to sum things up

We do not divide the inequality on both sides by the variables.

And yet….

Fun fact

If – otherwise – we had information that the variable (or the entire expression) by which we want to multiply/divide is always positive (or negative), we can boldly multiply/divide.

For example, if the function domain (there will be a review post about the function domain later) is a set of numbers , then we know that is definitely positive.

Then WE CAN do as follows…

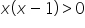$x open parentheses x minus 1 close parentheses greater than 0$ /:x

$x minus 1 greater than 0$

…remembering, however, to include the domain in the obtained solution set (and only take the solutions from .

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.