Directional derivatives – something new again?

---

Place and Time of Action

Calculating directional derivatives as a topic for study (i.e., for credit) is actually situated right after partial derivatives of multivariable functions, which most students cover in the second semester.

It’s a topic rarely tackled, so I didn’t include it in my Course on Partial Derivatives, but it’s common enough that I’ll throw it on the blog – for the benefit of those who need to learn directional derivatives and those who are simply curious about what it’s all about. However, like in the courses, today I’ll focus almost exclusively on practice (“how do I do this?”), not on theory (“what am I actually doing?”).

Directional Derivatives – How Do I Do This?

In the case of a directional derivative, we are dealing with the simultaneous increase of the x and y arguments, which of course corresponds to a certain increase in the value of the function .

For the task, we need three things:

1. The function from which we’ll calculate the directional derivative.
2. The point at which we’ll calculate the directional derivative.
3. The direction given in the form of a vector.

With the above, the task boils down to converting the vector into a directional vector (something from analytic geometry, I’ll show how to do it in a moment), and then plugging it into the formula:

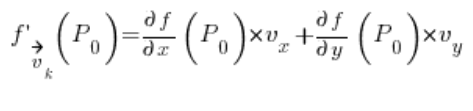
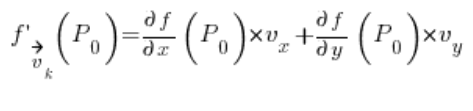
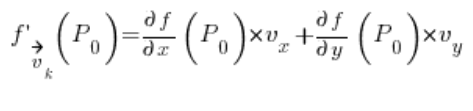
In which:

is the directional derivative at point in the direction of vector

is the point at which we calculate the directional derivative

are the coordinates of the directional vector

are the partial derivatives of the function at point .

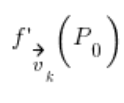
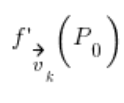
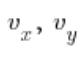
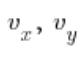
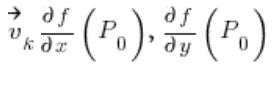
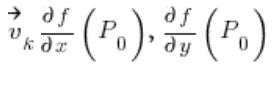
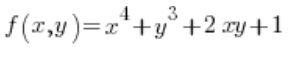
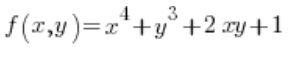
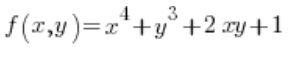
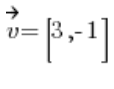
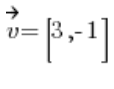
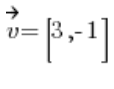
Calculate the directional derivative of the function at point P(1,2) in the direction .

Solution:

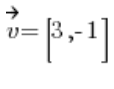
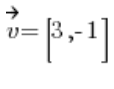
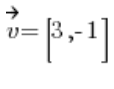
Everything is ready, we just need to turn the vector into a directional vector.

A directional vector is a vector with the same direction (who would’ve thought), same orientation, but with a length of 1.

It is calculated by the formula:

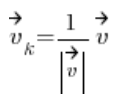
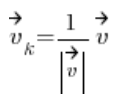
Simply put, divide its coordinates by its length.

So we calculate the length of the vector :

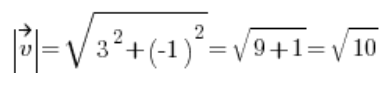
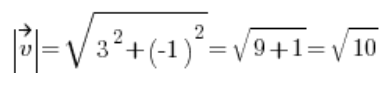
Then we get the directional vector:

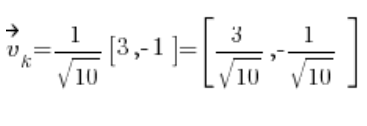
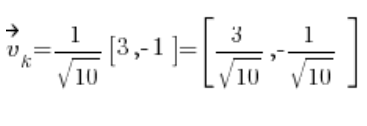
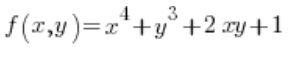
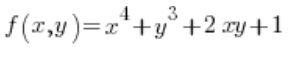
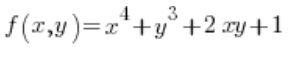
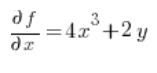
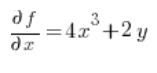
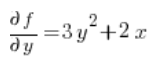
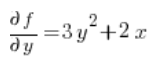
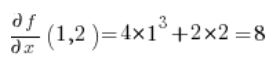
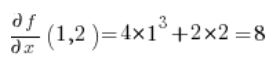
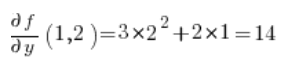
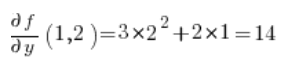
For the formula of the directional derivative, we also need the partial derivatives of the function at point P(1,2):

Now we have everything needed for the formula:

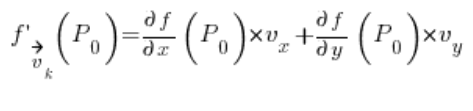
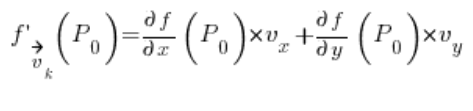
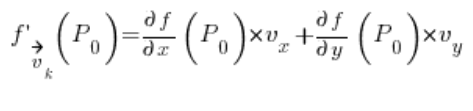
Just substitute and we have the result: .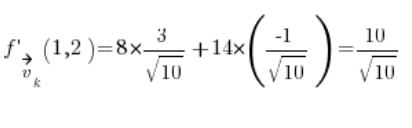

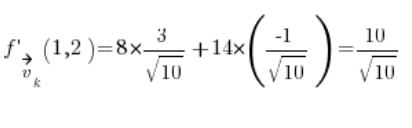
Done.

Example 2

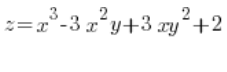
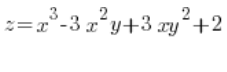
Find the directional derivative of the function: at point P(3,1) in the direction from this point to point Q(6,5).

Solution:

The task is a bit more difficult because the direction vector is not given directly, but no big deal.

We move from point P to point Q, so the shift vector is [3,4].

Now we find the directional vector by calculating the length of the vector [3,4]:

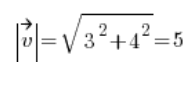
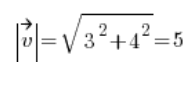
And we have the directional vector:

Now we calculate the partial derivatives at point (3,1):

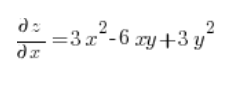
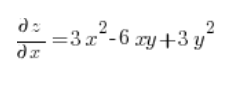
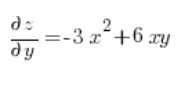
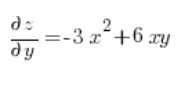
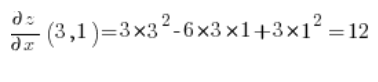
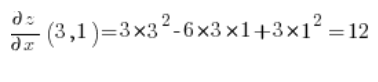
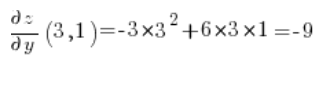
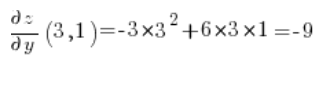
Then we just substitute into the formula for the directional derivative:

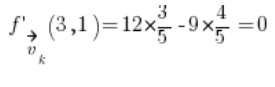
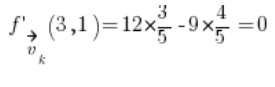
Example 3

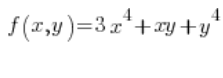
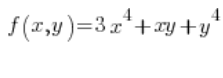
Find the directional derivative of the function at point (1,2) in the direction forming an angle with the positive x-axis.

Solution:

The task seems more difficult, due to the lack of a direction vector in the data. Let’s draw the whole thing:

It’s about finding the coordinates of any vector in the specified direction.

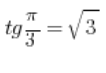
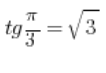
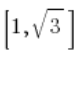
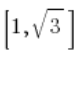
We use the fact that and we can assume that our vector has coordinates , as in the drawing (it was enough to choose any vector in the direction of the line):

And now we proceed as usual.

We calculate the directional vector:

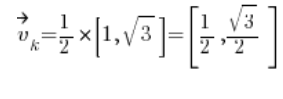
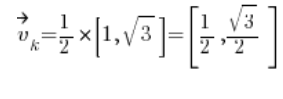
Then the partial derivatives at point (1,2):

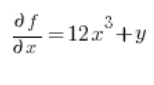
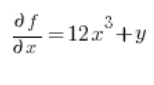
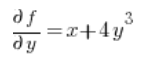
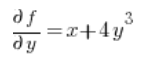
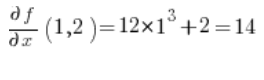
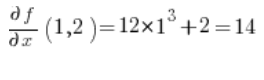
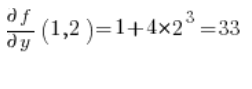
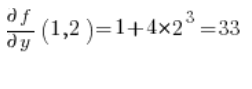
Substitute into the formula and we have the result

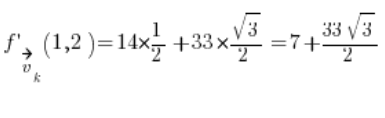
Feel free to ask questions in the comments – as always 🙂