No products in the cart.
Krystian Karczyński- 24 June 2024
- Komentarz 0
Harder function limits to calculate often require substitution, for example:
Example
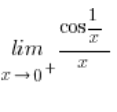
The limit in the numerator does not exist, in the denominator it approaches zero… What does the whole thing approach?
A convenient substitution would be: 
From the substitution, it follows that: 
And that if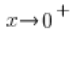 
, then 
. So we have:
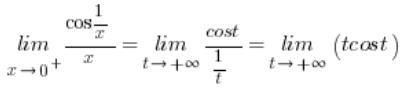
And this limit does not exist, which can be proven in the manner shown in another of my posts.
