Two types of discontinuity (function limits)
Krystian Karczyński
Founder and General Manager of eTrapez.
Graduate of Mathematics at Poznan University of Technology. Mathematics tutor with many years of experience. Creator of the first eTrapez Courses, which have gained immense popularity among students nationwide.
He lives in Szczecin, Poland. He enjoys walks in the woods, beaches and kayaking.
Continuity of functions at a point
As we all know, function
is continuous at a point 
, When:
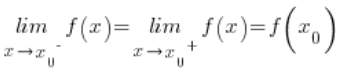
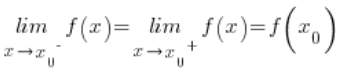
That is, whenthe limit of this function from below at this point is equal to the limit of the function from above at this point is equal to the value of the function at this point.
If any of the equality is not satisfied, the function is discontinuous at a point , and the point is called the discontinuity .
In this naming, you can go a step further and DISTINGUISH the discontinuities. We do it like this:
Discontinuity of the first type
Discontinuity we call it discontinuity of type I if the limits 
are finite (i.e. they are simply numbers).
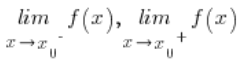
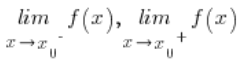
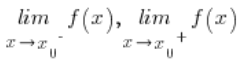
Additionally, if these limits are equal, then the point of discontinuity of type I is called removable .
Points of discontinuity of the second type
Discontinuity we call a type II discontinuity if some of the limits is not finite (i.e. it simply equals infinity plus or minus).
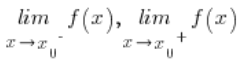
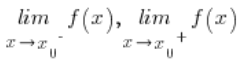
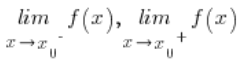
Example 1
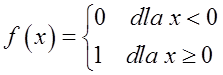
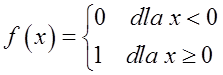
This function has a point 
discontinuity (because the below boundary at this point is 0 and the above boundary is 1 ). This is discontinuity of the first type, because the below and above limits at this point are finite (0 and 1). However this is not a removable discontinuity, because the limits are not equal.
Example 2
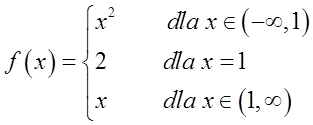
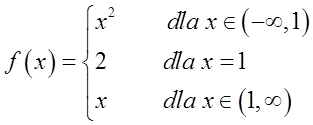
This function has a point 
discontinuity (because the below and above limits at this point are not equal to the value of the function at this point). This is a discontinuity of the first type, because the below and above limits are finite (and equal to 1). This is a removable discontinuity of the first type, because the below and above limits are equal.
Example 3
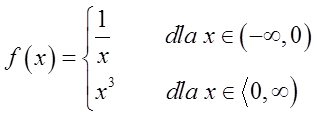
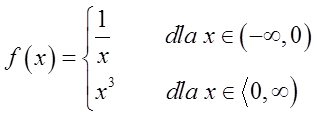
This function has a point discontinuity (because the below and above limits at this point are not equal). This is a point of type II discontinuity, because the below limit at this point is equal
.
Are you looking for college or high school math tutoring? Or maybe you need a course that will prepare you for the final exam?
We are "eTrapez" team. We teach mathematics in a clear, simple and very precise way - we will reach even the most knowledge-resistant students.
We have created video courses translated in an easy, understandable language, which can be downloaded to your computer, tablet or phone. You turn on the video, watch and listen, just like during private lessons. At any time of the day or night.
