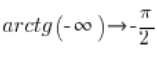Umgekehrte trigonometrische Funktionen (Vorlesung)
Thema: Umgekehrte trigonometrische Funktionen
Zusammenfassung
In dieser Vorlesung werde ich das Konzept der umgekehrten trigonometrischen Funktionen vorstellen: arcsinx, arccosx, arctgx, arcctgx. Dies sind die umgekehrten Funktionen der trigonometrischen Funktionen.
Die Vorlesung besteht aus zwei Teilen. Im ersten Teil zeige ich nur, wie man die Werte der umgekehrten trigonometrischen Funktionen schnell berechnet, ohne zu sehr ins Detail zu gehen (zu diesem Teil gibt es ein Video, ein Ausschnitt aus meinem Integralrechnungskurs).
Im zweiten Teil beschreibe ich die umgekehrten trigonometrischen Funktionen genauer, zeige ihre Graphen usw.
Zum Verständnis der Vorlesung werden benötigt:
- trigonometrische Funktionen (Gymnasium)
Teil I
Umgekehrte trigonometrische Funktionen – „INSTANT“-Version
Umgekehrte trigonometrische Funktionen sind einfach gesagt die umgekehrten Funktionen der trigonometrischen Funktionen. Also ist arcsinx die umgekehrte Funktion von sinx.
Das bedeutet, wenn wir zum Beispiel wissen, dass 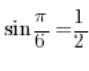 , dann bedeutet das, dass
, dann bedeutet das, dass ![]() .
.
Und so weiter:
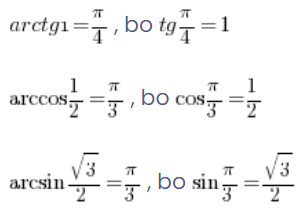
Dazu haben wir noch einige Eigenschaften der umgekehrten trigonometrischen Funktionen, die es uns ermöglichen, ihre Werte auch für negative Argumente zu berechnen:
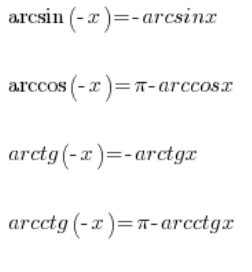
Also können wir das auch noch berechnen:
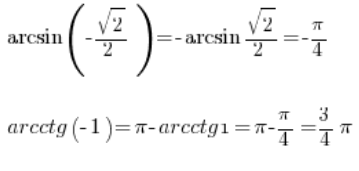
Mit einer Tabelle der trigonometrischen Funktionen können wir die Werte der umgekehrten trigonometrischen Funktionen ganz einfach bestimmen, indem wir sie einfach „umgekehrt“ lesen.
Ich erkläre das genauer im Video hier:
Tabelle der grundlegenden trigonometrischen Funktionswerte aus dem Video – hier herunterladen.
Teil II
Umgekehrte trigonometrische Funktionen – vollständige Version
Einleitung – Warum Teil I nicht ausreicht
Es sieht so aus, als hätten wir in Teil I jede umgekehrte trigonometrische Funktion als umgekehrte Funktion der entsprechenden trigonometrischen Funktion definiert.
Lassen Sie uns das etwas formalisieren. Wir haben gesagt, dass die Funktion ![]() den Wert
den Wert ![]() annimmt, wenn die Funktion
annimmt, wenn die Funktion ![]() dieses
dieses ![]() den Wert
den Wert ![]() hat.
hat.
Entsprechend:
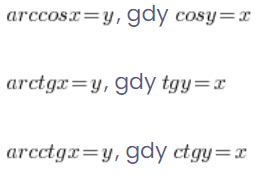
Also wenn wir ![]() berechnen wollen, denken wir darüber nach, welcher Winkel den Cosinus von
berechnen wollen, denken wir darüber nach, welcher Winkel den Cosinus von ![]() ergibt, wir erkennen, dass es der Winkel
ergibt, wir erkennen, dass es der Winkel ![]() ist und wir haben das Ergebnis:
ist und wir haben das Ergebnis: 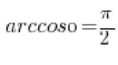 .
.
Deckt das alle Werte der umgekehrten trigonometrischen Funktionen ab?
Natürlich NICHT.
Lassen Sie uns die Überlegungen noch einmal mit konkreten Zahlen durchgehen (und vielleicht traditionell zu arcsinx wechseln):
Wenn wir  berechnen wollen, denken wir darüber nach, welcher Winkel den Sinus von
berechnen wollen, denken wir darüber nach, welcher Winkel den Sinus von ![]() ergibt, wir erkennen, dass es der Winkel
ergibt, wir erkennen, dass es der Winkel ![]() ist und wir haben das Ergebnis:
ist und wir haben das Ergebnis:  .
.
Wo liegt das Problem? Im fettgedruckten Teil:
Wenn wir  berechnen wollen, denken wir darüber nach, welcher Winkel den Sinus von
berechnen wollen, denken wir darüber nach, welcher Winkel den Sinus von ![]() ergibt, wir erkennen, dass es der Winkel
ergibt, wir erkennen, dass es der Winkel ![]() ist und wir haben das Ergebnis:
ist und wir haben das Ergebnis:  .
.
Leider ist nicht nur der Sinus von ![]() gleich
gleich ![]() .
.
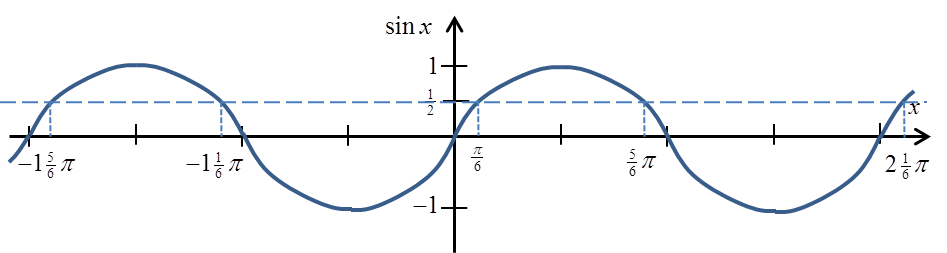
Lassen Sie uns das Diagramm der Sinusfunktion erinnern (ich habe den Wert ![]() darauf markiert):
darauf markiert):
Wir sehen und wissen aus dem Gymnasium, dass der Sinus den Wert ![]() nicht nur für den Winkel
nicht nur für den Winkel ![]() annimmt, sondern auch für die Winkel:
annimmt, sondern auch für die Winkel: 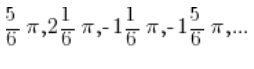
Das bedeutet 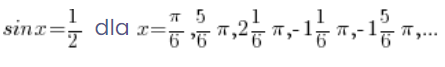
Lassen Sie uns unsere Methode zur Berechnung von arcsin erinnern:
Wenn wir  berechnen wollen, denken wir darüber nach, welcher Winkel den Sinus von
berechnen wollen, denken wir darüber nach, welcher Winkel den Sinus von ![]() ergibt, wir erkennen, dass es der Winkel
ergibt, wir erkennen, dass es der Winkel ![]() ist und wir haben das Ergebnis:
ist und wir haben das Ergebnis:  .
.
Aber jetzt wissen wir, dass nicht nur sin![]() gleich
gleich ![]() ergibt, also sieht es so aus:
ergibt, also sieht es so aus:
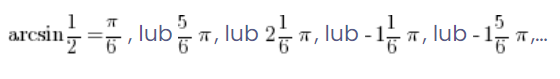
Das würde bedeuten, dass arcsinx überhaupt keine Funktion ist, weil einem Argument mehrere Werte zugeordnet sind!
Eine eindeutige Antwort auf die Frage, wie viel arcsin von etwas ist, wäre dann völlig unmöglich.
Es ist auch leicht vorstellbar, dass ein ähnliches Problem bei JEDER der trigonometrischen Funktionen besteht.
Fachlich ausgedrückt: Diese Funktionen sind nicht eindeutig, daher existieren keine Umkehrfunktionen für sie. Bei jeder trigonometrischen Funktion wird jeder Wert für eine unendliche Anzahl von Argumenten erreicht (sie sind periodisch, richtig?), daher erhalten wir bei dem Versuch, ihre Umkehrfunktionen zu bestimmen, eine unendliche Anzahl von Werten für jedes Argument. Und das kann bei Funktionen nicht sein.
Was tun?
Es ist ziemlich einfach, um nicht zu sagen primitiv. Jede der trigonometrischen Funktionen kann so GESCHNITTEN werden, dass das Ergebnis eine eindeutige Funktion ist.
Also definieren wir alle 4 zyklometrischen Funktionen korrekt:
arcsinx
Erinnern wir uns an das Diagramm der sinx-Funktion:
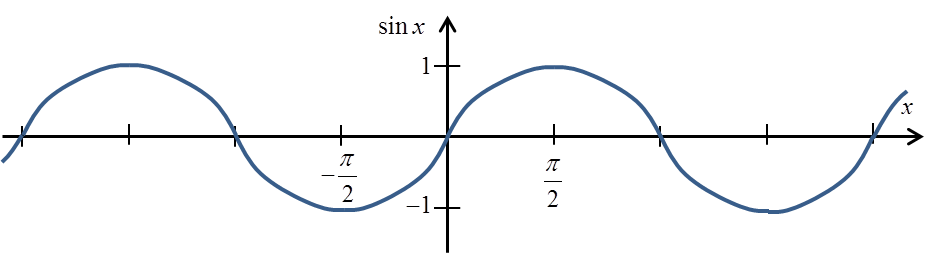
Wenn wir uns einigen, dass wir es zum Beispiel auf das Intervall ![]() kürzen, erhalten wir ein solches Diagramm:
kürzen, erhalten wir ein solches Diagramm:
![Wykres sinx w przedziale [0,pi] Obraz3](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz33.png)
Leider ist das nicht das, was wir wollen, weil es immer noch nicht das Diagramm einer eindeutigen Funktion ist, und das Problem mit dem Wert ![]() besteht weiterhin:
besteht weiterhin:
![Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2 Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz41.png)
Also einigen wir uns darauf, die sinx-Funktion anders zu kürzen, auf die Argumente 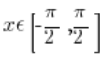 :
:
![Wykres funkcji sinx dla x należących do [-pi/2,pi/2] Wykres funkcji sinx dla x należących do [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz51.png)
Jetzt ist es eine eindeutige Funktion und hat eine Umkehrfunktion arcsinx.
Das Diagramm der arcsinx-Funktion sieht ungefähr so aus:

Ihr Definitionsbereich ist das Intervall ![]() existiert nicht.
existiert nicht.
Die genaue Definition der arcsinx-Funktion ist daher:
![]() .
.
arccosx
Die cosx-Funktion ist ebenfalls keine eindeutige Funktion:
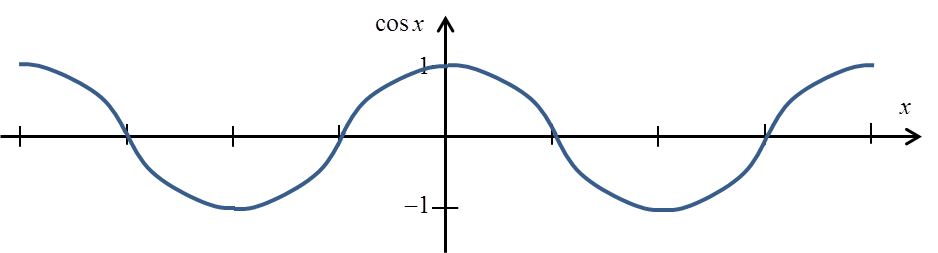
Um eine eindeutige Funktion zu erhalten, müssen wir sie jedoch auf das Intervall ![]() kürzen:
kürzen:
![Wykres funkcji cosx obciętej do przedziału [0,pi] Wykres funkcji cosx obciętej do przedziału [0,pi]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz8.png)
So definiert ist die Funktion bereits eindeutig und hat eine Umkehrfunktion arccosx.
Ihr Diagramm sieht ungefähr so aus:
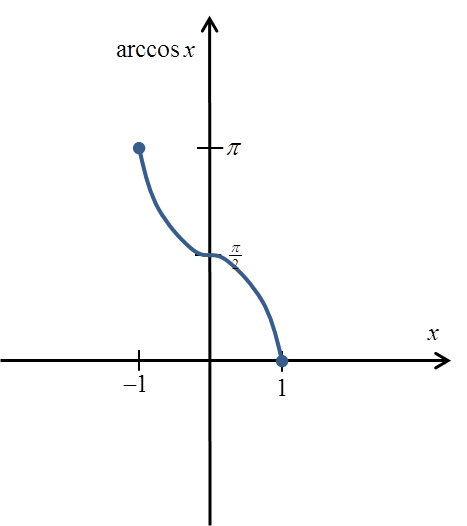
Und ihre genaue Definition:
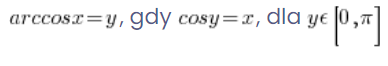 .
.
arctgx
Das Diagramm der tgx-Funktion sieht so aus:

Es ist auch keine eindeutige Funktion! Wir können sie wie folgt kürzen:
![Wykres funkcji tgx obięty do przedziału [-pi/2,pi/2] Wykres funkcji tgx obięty do przedziału [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz111.png)
So erhalten wir eine eindeutige Funktion.
Das Diagramm der arctgx-Funktion sieht so aus:

Und ihre genaue Definition ist:
![]() , für y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right).
, für y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right).
Wir bemerken auch, dass aus dem Diagramm einige interessante Eigenschaften hervorgehen, z.B.:
- Der Definitionsbereich der arctgx-Funktion ist die Menge der reellen Zahlen (wir können arctg von jeder Zahl berechnen)


arcctgx
Aus dem Diagramm der ctgx-Funktion:

Schneiden wir ein eindeutiges Stück heraus:
Das Diagramm der arcctgx-Funktion sieht so aus:
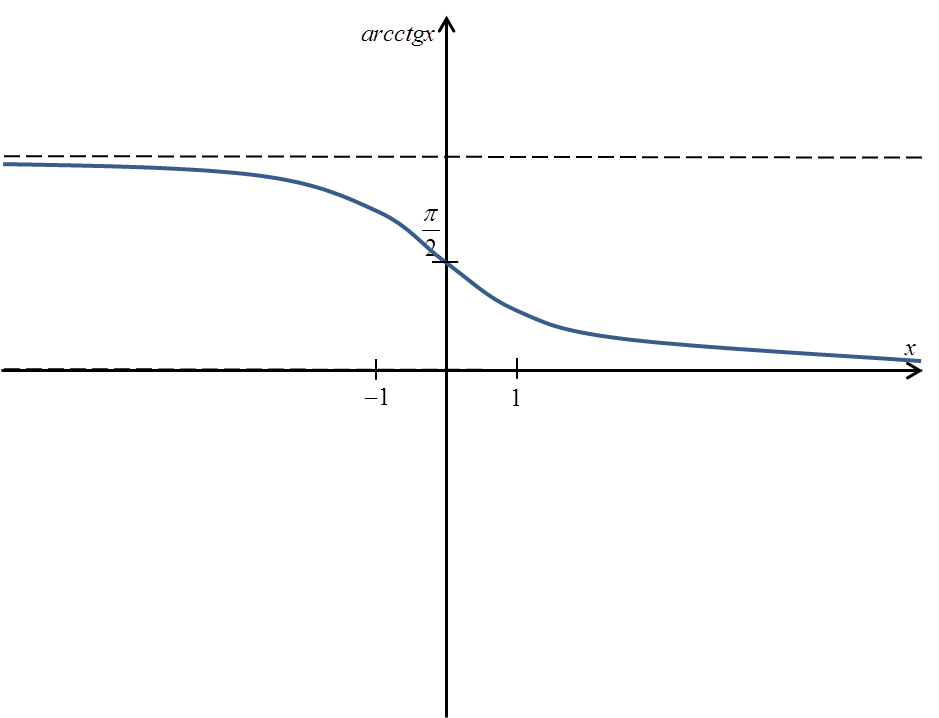
Die genaue Definition von arcctgx wäre:
![]() .
.
Wir sehen, dass:
- Der Definitionsbereich der arcctgx-Funktion ist die Menge der reellen Zahlen (wir können arcctg von jeder Zahl berechnen)


Hinweis
In vielen Taschenrechnern und mathematischen Notationen im Allgemeinen (insbesondere westlichen) werden die Umkehrfunktionen der trigonometrischen Funktionen nicht als „arcus“ bezeichnet, sondern durch den Exponenten -1. Zum Beispiel wird arcsinx als ![]() geschrieben. Wenn man weiß, worum es geht, ist das kein Problem. Man kann jedoch einen schrecklichen Fehler machen und die Umkehrfunktion von sinx mit der Funktion
geschrieben. Wenn man weiß, worum es geht, ist das kein Problem. Man kann jedoch einen schrecklichen Fehler machen und die Umkehrfunktion von sinx mit der Funktion ![]() verwechseln – die eine völlig andere Funktion als arcsinx ist.
verwechseln – die eine völlig andere Funktion als arcsinx ist.