Warum kann der Graph einer Funktion keine zwei schiefen Asymptoten haben, wenn x gegen plus Unendlichkeit strebt?
Krystian Karczyński
Gründer und Chef des Dienstes eTrapez.
Master of Mathematics der Technischen Universität Pozen (Polen). Mathematik-Nachhilfelehrer mit langjähriger Erfahrung. Schöpfer der ersten eTrapez-Kurse, die bei Studenten in ganz Polen große Beliebtheit erlangten.
Lebt in Stettin (Polen). Mag Waldspaziergänge, Strandtage und Kajakfahren.
Um die im Titel gestellte Frage zu beantworten, müssen wir nicht auf die Definition einer schiefen Asymptote zurückgreifen, es reicht zu wissen, was eine Funktion ist.
Wie so oft in der Mathematik stellen wir uns vor, dass der Graph der Funktion zwei verschiedene schräge Asymptoten bei 
hat und zeigen, dass diese Annahme definitiv zu einem Widerspruch führt, daher kann diese Annahme nicht akzeptiert werden.
Graph
Im Graphen könnten diese Asymptoten zum Beispiel so aussehen:
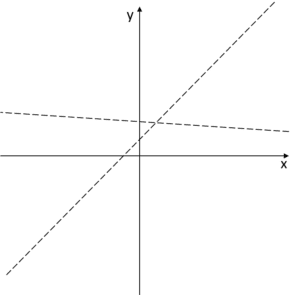Der Graph der Funktion sollte sich diesen Asymptoten bei annähern, und würde daher so aussehen:
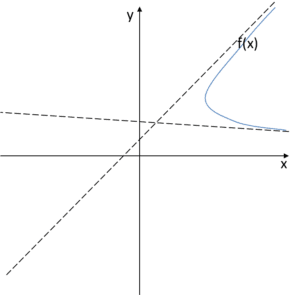Und, was denkt ihr? Kann das so sein? Kann der Graph einer Funktion so aussehen? Oder haben wir hier ein Problem?
Problem
Natürlich haben wir ein Problem. Was oben gezeigt ist, kann kein Graph einer Funktion sein. Schauen wir uns die Definition an, eine Funktion ist per Definition eine Zuordnung, die jedem Argument x genau einen Wert y zuordnet. Was ergibt sich aus unserem Graphen?
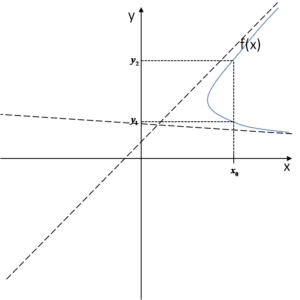Wir können daraus ablesen, dass zum Beispiel dem Argument 
zwei Werte zugeordnet sind – 
und 
. Das kann in einem Funktionsgraphen nicht sein, denn jedem Argument x muss nur ein Wert y zugeordnet sein.
Daher kann eine Funktion bei keine zwei verschiedenen schiefen Asymptoten haben. Das gesamte Argument lässt sich entsprechend für 
wiederholen 🙂
Suchen Sie nach Mathe-Nachhilfe für das Universitätsniveau oder die Oberstufe? Oder benötigen Sie vielleicht einen Kurs, der Sie auf das Abitur vorbereitet?
Wir sind das Team von eTrapez. Wir unterrichten Mathematik auf eine klare, einfache und sehr detaillierte Weise - wir erreichen sogar diejenigen, die sich am meisten gegen das Lernen sträuben.
Wir haben Kurse in Videoform erstellt, die in einer verständlichen Sprache erklärt sind, zum Herunterladen auf Computer, Tablet oder Handy. Sie starten die Aufnahme, schauen und hören zu, als wären Sie bei der Nachhilfe. Zu jeder Tages- und Nachtzeit.
