Wir haben den Grenzwert einer Funktion:
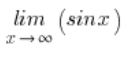
Intuitiv fühlen wir, dass der obige Grenzwert nicht existiert. Die x-Werte werden immer größer und größer, und die Sinuswerte „schwanken” ständig zwischen -1 und 1.
Formaler Beweis
Aber wie beweisen wir das formal?
Aus der Definition des Grenzwerts einer Funktion, wenn x gegen unendlich geht wissen wir, dass ein Grenzwert existiert, wenn für jede Folge von Argumenten der Funktion, die gegen 
divergiert, die entsprechende Folge von Funktionswerten gegen dieselbe Zahl konvergiert (dann ist diese Zahl der Grenzwert).
Um zu zeigen, dass ein solcher Grenzwert nicht existiert, genügt es, zwei beliebige Folgen von Argumenten zu nehmen, die gegen divergieren, und zu zeigen, dass die entsprechenden Folgen von Werten gegen zwei verschiedene Zahlen konvergieren.
Wir wissen, dass die Sinusfunktion periodisch ist, daher können diese Folgen beispielsweise sein:
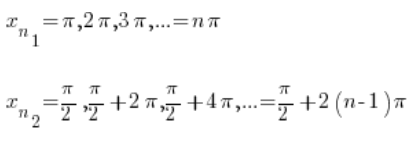
Natürlich divergieren beide Folgen gegen unendlich, wenn 
.
Schauen wir uns nun die Folgen von Funktionswerten an, die diesen Folgen entsprechen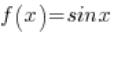 
:
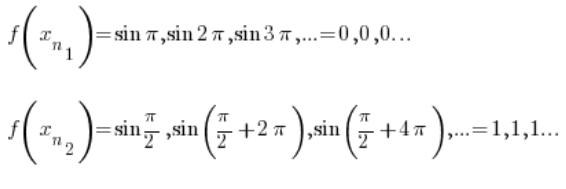
Natürlich konvergiert die erste Folge gegen 0 und die zweite Folge gegen 1.
Das genügt, um zu beweisen, dass der Grenzwert der Funktion:
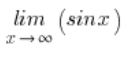
nicht existiert.
