Horizontale und schiefe Asymptoten von Funktionen
Krystian Karczyński
Gründer und Chef des Dienstes eTrapez.
Master of Mathematics der Technischen Universität Pozen (Polen). Mathematik-Nachhilfelehrer mit langjähriger Erfahrung. Schöpfer der ersten eTrapez-Kurse, die bei Studenten in ganz Polen große Beliebtheit erlangten.
Lebt in Stettin (Polen). Mag Waldspaziergänge, Strandtage und Kajakfahren.
Der Zusammenhang zwischen horizontalen und schrägen Asymptoten ist folgender: Horizontale Asymptoten sind ein spezieller Fall von schrägen Asymptoten. Jede horizontale Asymptote ist also eine schräge, aber nicht jede schräge ist eine horizontale.
Man kann und sollte dies nutzen, um sich das Berechnen von Asymptoten der Funktion zu erleichtern. Es gibt grundsätzlich zwei Ansätze zu diesem Thema:
1. Zuerst berechnen wir die horizontalen Asymptoten
Dieser Ansatz wird in meinem Videokurs über das Verhalten von Funktionen gezeigt.
Die Bedingung für das Vorhandensein einer horizontalen Asymptote einer Funktion ist:
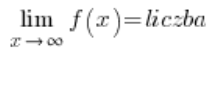oder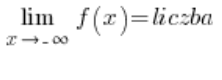 
Wenn horizontale Asymptoten auftreten, berechnen wir keine schiefen Asymptoten mehr (da es so ist, als ob die schiefen bereits bestimmt wurden – denken Sie daran, dass horizontale eine Art von schiefen sind). Wenn jedoch keine horizontalen Asymptoten erscheinen, haben wir ein Problem – wir müssen die schiefen Asymptoten neu berechnen.
Natürlich ist die Situation etwas komplizierter: Eine horizontale Asymptote könnte bei 
„auftreten“ und bei 
„nicht auftreten“. In solchen Fällen würden wir die Existenz einer schiefen Asymptote bei nicht untersuchen (da sie dort bereits erschienen ist), aber wir müssten ihre Anwesenheit bei überprüfen.
2. Zuerst berechnen wir die schiefen Asymptoten
…und dann erscheinen die horizontalen Asymptoten automatisch (oder auch nicht); wir müssen nur die Ergebnisse richtig interpretieren. Dieser Ansatz wird in meinem Kurs nicht gezeigt. Der Nachteil ist, dass die Bedingungen für das Vorhandensein einer schiefen Asymptote einer Funktion etwas komplizierter si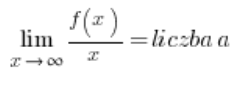nd:
und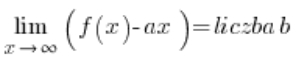 
oder:
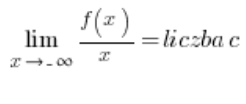und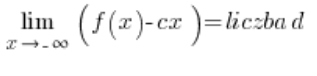 
…und der Vorteil ist, dass man danach nichts weiter berechnen muss. Wenn die Bedingungen erfüllt sind und die Zahl 
(oder 
) aus den Bedingungen für die Existenz einer schiefen Asymptote gleich 
ist, bedeutet dies, dass die schiefe Asymptote tatsächlich eine horizontale Asymptote ist.
Um uns die Arbeit weiter zu erleichtern, können wir direkt berechnen:
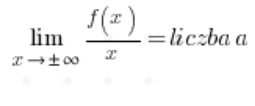und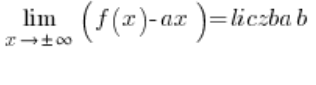 
Und die Berechnung der Bedingungen für 
und 
nur dann separat durchführen, wenn es notwendig ist (wenn es einen Unterschied im Ergebnis macht, ob x gegen oder gegen strebt).
Suchen Sie nach Mathe-Nachhilfe für das Universitätsniveau oder die Oberstufe? Oder benötigen Sie vielleicht einen Kurs, der Sie auf das Abitur vorbereitet?
Wir sind das Team von eTrapez. Wir unterrichten Mathematik auf eine klare, einfache und sehr detaillierte Weise - wir erreichen sogar diejenigen, die sich am meisten gegen das Lernen sträuben.
Wir haben Kurse in Videoform erstellt, die in einer verständlichen Sprache erklärt sind, zum Herunterladen auf Computer, Tablet oder Handy. Sie starten die Aufnahme, schauen und hören zu, als wären Sie bei der Nachhilfe. Zu jeder Tages- und Nachtzeit.
