Als Kuriosität berechne ich den Grenzwert der Funktion:
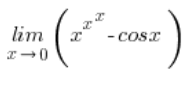
Interessanter als die Berechnungen selbst sind die beiden Lehren, die man daraus ziehen kann. Aber die Lehren kommen am Ende (hat jemand schon mal eine Geschichte mit einer Lehre am Anfang gesehen)? Jetzt berechne ich:
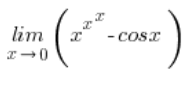
Zunächst schaue ich, worauf das hinausläuft, und ich habe:
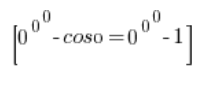
Das heißt, ich habe keine Ahnung, worauf das hinausläuft, weil ich nicht einmal weiß, worauf 
hinausläuft (das ist ein unbestimmtes Symbol), geschweige denn so etwas Seltsames wie: 
.
Es sieht jedoch so aus, als gäbe es mit dem Kosinus keine Probleme, also berechne ich am Rand, worauf das hinausläuft:
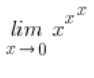
Ich werde die Regel von L’Hôpital anwenden (ich habe genau erklärt, worum es in meinem Kurs geht), das heißt, ich werde die Formel (
) verwenden:
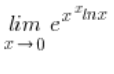
Aber es ist immer noch nicht gut, weil ich im Exponenten weiterhin ein unbestimmtes Symbol 
habe, also transformiere ich es ein zweites Mal:
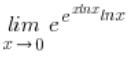
Jetzt kann ich ruhig anfangen zu arbeiten. Ich berechne am Rand:
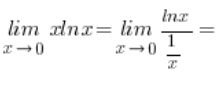
, also habe ich ein unbestimmtes Symbol 
, also wende ich L’Hôpital an:
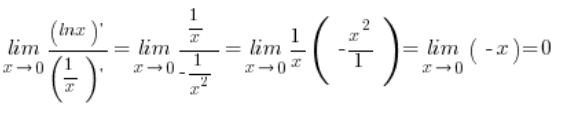
Das heißt, ich habe am Rand berechnet, dass: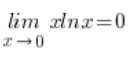 
.
Zurück zum Grenzwert:
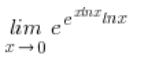
Ich weiß jetzt, dass ich in der Situation bin:
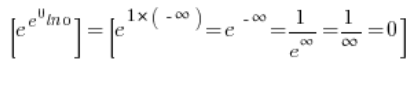
Das heißt, es stellt sich heraus, dass:
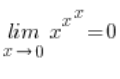
Also ist mein ganzer Grenzwert:
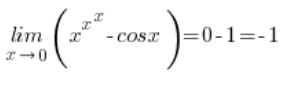
Und der Kosinus war nur zum Spaß.
Lehren aus dieser Geschichte
Es gibt zwei.
- Bei schwierigeren Grenzwerten kann man immer und manchmal muss man ein Stück davon nehmen und berechnen, wohin es „am Rand“ geht.
- Manchmal können bestimmte Teile der Grenzwertformel wie dieser Kosinus hinzugefügt werden. Es stellte sich heraus, dass ich damit nichts machen musste, nur am Ende null einsetzen.
