Die Grenze einer Sequenz mit der Zahl e… Wirklich?
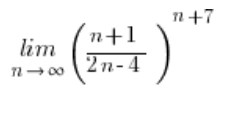
Wenn wir einige Aufgaben zur Sequenzgrenze gelöst haben, können wir in einen bestimmten Automatismus verfallen. Und wir beginnen, diese Grenze zu berechnen wie wir die Grenzen mit der Zahl e im Ergebnis berechnen: 4 im Zähler abziehen und hinzufügen, in zwei Brüche teilen usw. Doch so gelangen wir zu einem kleinen Problem…
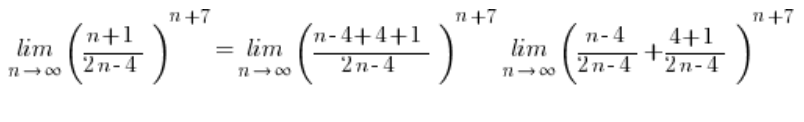
Dieses Mal kürzt sich der erste Bruch gar nicht und ergibt kein Eins!
Lehrer gehen oft nicht ins Detail, aber wir verwenden die Grenzen mit der Zahl e im Ergebnis, wenn es eine unbestimmte Form 
gibt, und in unserem Beispiel:
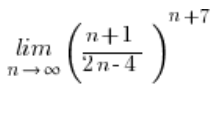
Zweiter Teil:
Der Quotient von Polynomen, der zu Potenzen erhoben wird, tendiert keineswegs zu 1, sondern zu 
, wie man durch Herausziehen der größten Potenzen außerhalb der Klammern sehen kann:
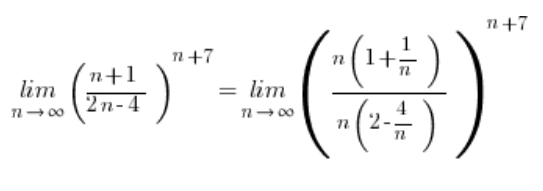
Also haben wir eine Situation 
, und diese Art der Sequenzgrenze ist 0:
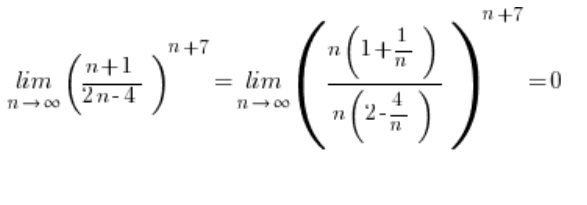
Das Problem mit diesen Arten von Grenzen
Bevor du dich also mit den Grenzen von Sequenzen durch Formeln mit der Zahl e beschäftigst, lohnt es sich zu überlegen, ob der Ausdruck, der zu Potenzen erhoben wird, überhaupt zu 1 tendiert. Im Falle der Division eines Polynoms durch ein anderes kann man dies leicht prüfen, ohne Berechnungen durchzuführen. Diese Division tendiert zu 1, wenn die höchsten Potenzen der Polynome gleich sind und auch die Koeffizienten vor ihnen gleich sind. In diesem Fall kannst du die Methode der Sequenzgrenze mit der Zahl e anwenden. Wenn nicht, musst du wahrscheinlich die größte Potenz herausziehen.
Beurteile selbst, auf einen Blick
Zum Schluss eine Übung. Schau dir die folgenden Grenzen an und beurteile „auf einen Blick“, welche mit der e-Formel gelöst werden müssen und welche durch Herausziehen der größten Potenz:
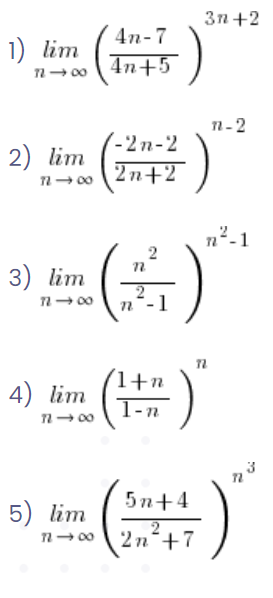
… und sie sehen alle so ähnlich aus… 🙂
