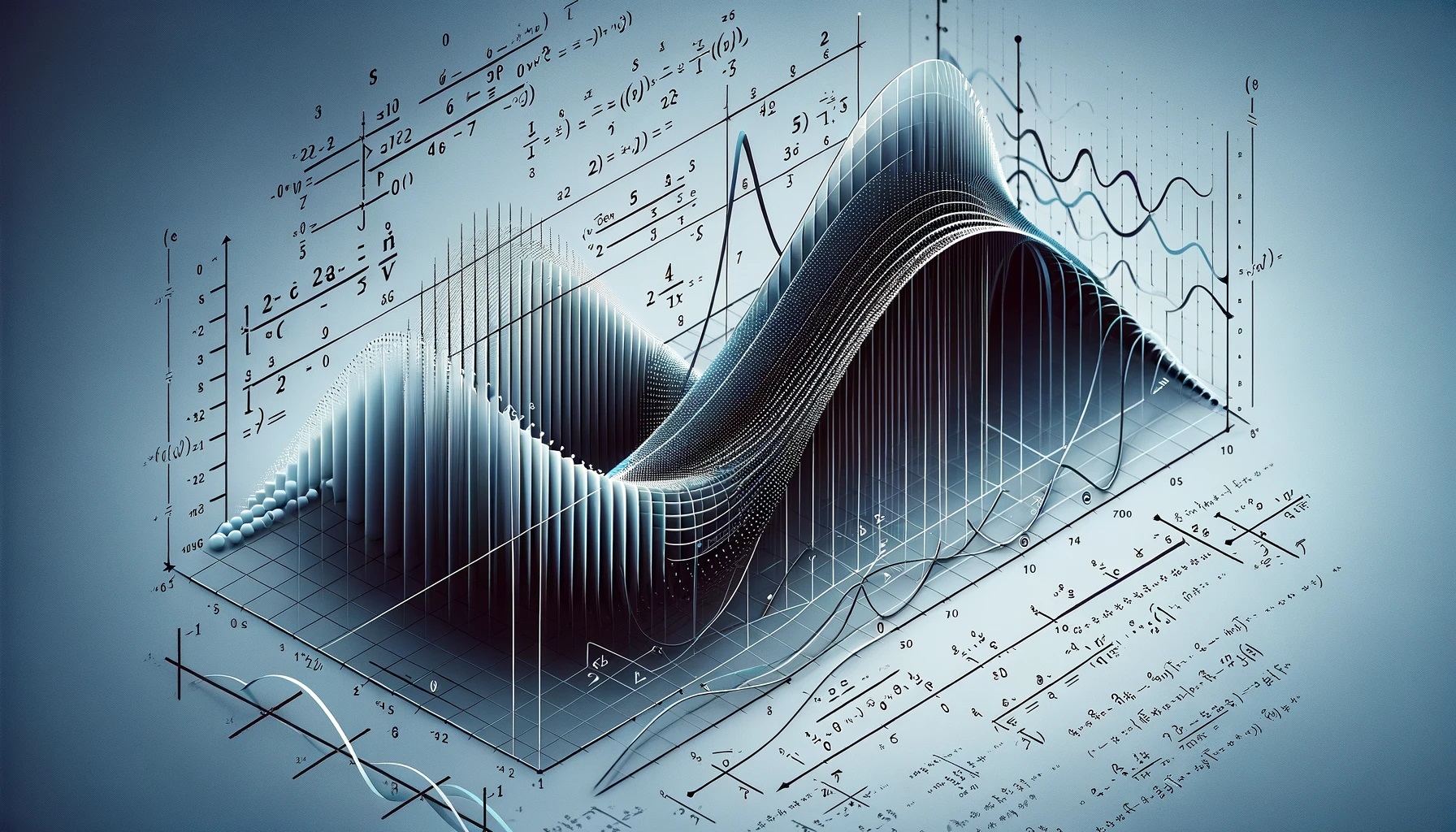
Granica ciągu udająca granicę z liczbą e
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Granica ciągu z liczbą e… czy rzeczywiście?
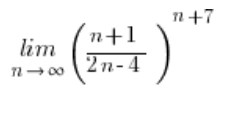
Jeśli mamy już trochę zadań z granic ciągu rozwiązanych, możemy popaść już w pewien automatyzm. I zabrać się za liczenie powyższej granicy, tak jak liczy się granice z wzorem na liczbę e w wyniku, tzn. odjąć i dodać 4 w liczniku, rozbić na dwa ułamki itd. Ale licząc tak dojdziemy do pewnego, delikatnie pisząc, problemu…
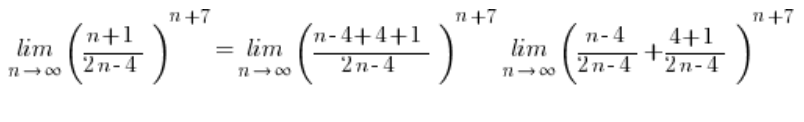
Tym razem pierwszy ułamek nie skraca się wcale i nie daje jedynki!
Nauczyciele często nie rozwodzą się nad tym zwykle, ale granice z liczbą e w wyniku stosujemy wtedy, gdy mamy symbol nieoznaczony ![]() a w naszym przykładzie:
a w naszym przykładzie:
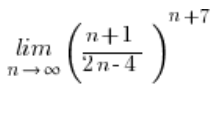
iloraz wielomianów podniesiony do potęgi nie dąży bynajmniej do 1, tylko do ![]() – o czym przekonać się można wyciągając w nim największe potęgi przed nawias:
– o czym przekonać się można wyciągając w nim największe potęgi przed nawias:
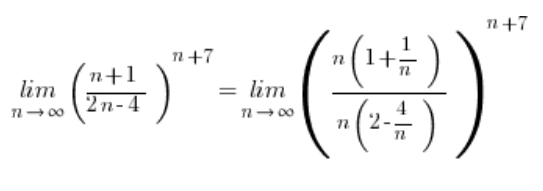
Mamy więc sytuację ![]() , a taka granica ciągu z odpowiedniego wzoru równa jest 0:
, a taka granica ciągu z odpowiedniego wzoru równa jest 0:
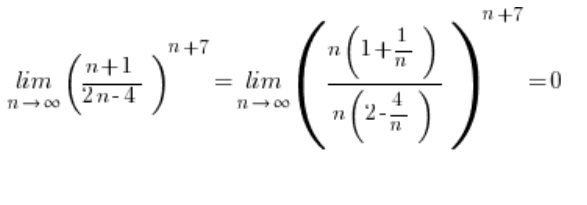
Problem z tego typu granicami
Zanim zaatakujesz więc granicę ciągu wzorami na liczbę e, warto się zastanowić, czy wyrażenie podniesione do potęgi dąży do 1 w ogóle. W przypadku dzielenia wielomianu przez wielomian można to sprawdzić łatwo, bez wykonywania obliczeń. To dzielenie dążyć będzie do 1, jeśli największe potęgi wielomianów będą takie same i współczynniki przy nich też będą takie same. Wtedy stosuj metodą na granicę ciągu z liczbą e. Jeśli tak nie jest – najprawdopodobniej trzeba wyciągać największą potęgę przed nawias.
Oceń sam, na oko
Na koniec ćwiczenie. Spójrz na poniższe granice i oceń “na oko”, które z nich trzeba rozwiązywać metodą granicy z liczbą e, a które metodą wyciągania przed nawias największej potęgi:
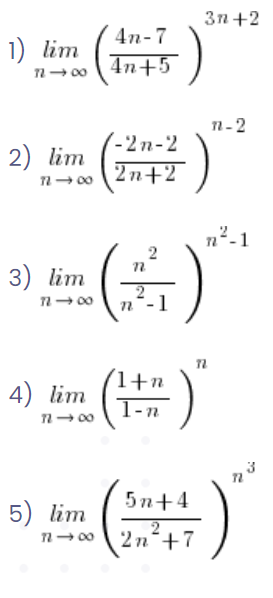
…a wszystkie wyglądają tak podobnie… 🙂
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.










Dzień dobry! Proszę o wyjaśnienie odpowiedzi do pytania 10 z testu. Z góry dziękuje!
chociaż faktycznie w opisanym przykładzie granica jest równa zero, ale dla uzasadnienia należałoby wyłączyć przed nawias w liczniku n, a w mianowniku 2n i mamy wyrażenie (1/2)^n oraz inne z zastosowaniem w granicy liczby e.
Zatem, idąc tym tokiem rozumowania, granica ciągu (1+1/n)^n powinna być równa 1, ponieważ 1 do potęgi nieskończoność jest równe 1…
Wiadomo, że granica ta jest równa e.
1 do potęgi nieskończoność jest symbolem nieoznaczonym i to jest cały problem…Co do komentarza niżej – nic takiego nie trzeba robić, bo to jest zwyczajna granica z ułamkiem, taka jaką się robi na pierwszych lekcjach z granic. Można ją policzyć w pamięci. To że jest podniesiona do potęgi nic nie zmienia, bo nie ma żadnego symbolu nieoznaczonego. Oczywiście można zrobić to co napisałeś, ale jest zupełnie niepotrzebnym komplikowaniem.Tak wiem, necroposting, ale odpowiadam na ten durny komentarz jakby ktoś się zastanawiał.