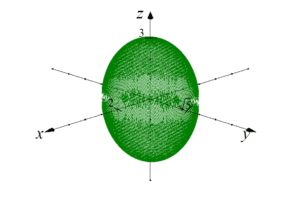
Das Volumen eines Ellipsoids (aber nicht eines Rotationsellipsoids, sondern eines wilden Typs) berechnet mit einem bestimmten Integral
Krystian Karczyński
Gründer und Chef des Dienstes eTrapez.
Master of Mathematics der Technischen Universität Pozen (Polen). Mathematik-Nachhilfelehrer mit langjähriger Erfahrung. Schöpfer der ersten eTrapez-Kurse, die bei Studenten in ganz Polen große Beliebtheit erlangten.
Lebt in Stettin (Polen). Mag Waldspaziergänge, Strandtage und Kajakfahren.
Angenommen, wir müssen das Volumen eines Ellipsoids berechnen:
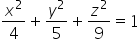
Dieses Ellipsoid schneidet die x, y, z-Achsen an den Koordinaten 2, 
und 3 (die allgemeine Gleichung des Ellipsoids ist: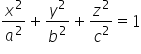 
, wobei a,b,c die Schnittkoordinaten sind).
Dies ist kein Rotationsellipsoid, es entsteht nicht durch Drehung einer Kurve um eine Achse, wir können also nicht die Standardformel für das Volumen eines Rotationskörpers verwenden:
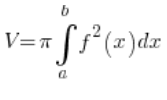
Wir müssen uns etwas anderes überlegen.
1. Wir wählen einen beliebigen Punkt M(z) im Zentrum des Ellipsoids und auf der OZ-Achse.
Eine Ebene, die durch diesen Punkt verläuft und senkrecht zur OZ-Achse steht, “schneidet” uns eine bestimmte Ellipse aus dem Ellipsoid:
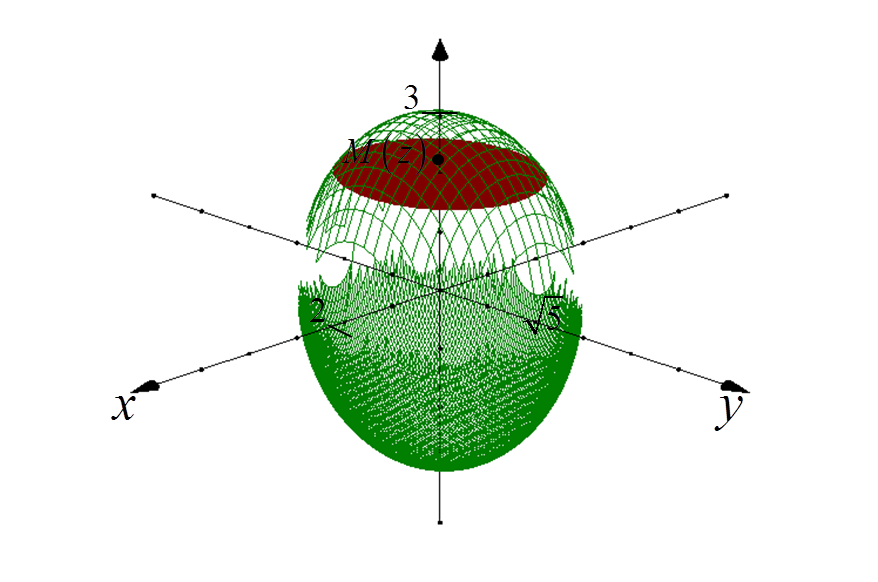
2. Bestimmen wir die Gleichung der “ausgeschnittenen” Ellipsenprojektion auf die XY-Ebene
Wir bestimmen die Gleichung dieser Ellipse für ein festes ‘z’ (behandeln ‘z’ als Konstante) aus der allgemeinen Gleichung des Ellipsoids:
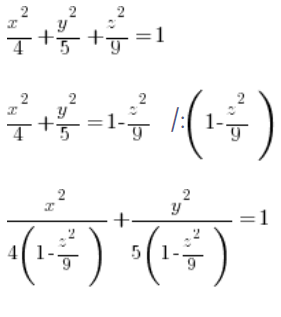
Man sieht, dass unser ‘a’ und ‘b’ aus der allgemeinen Gleichung des Ellipsoids (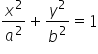
) sind:
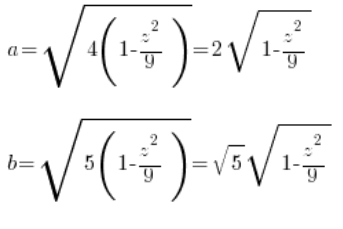
4. Berechnen wir die Fläche dieses Schnitts in Abhängigkeit von der Variablen ‘z’
Die Fläche dieser Ellipse hängt von dem gewählten Punkt ‘z’ ab, also wird es eine Funktion der Variablen ‘z’ sein. Wir können sie entweder mit der fertigen Formel für die Fläche der Ellipse berechnen (
):
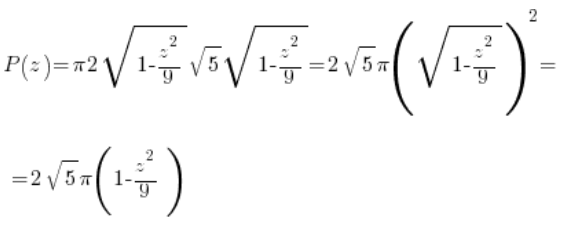
Oder durch mühsames Berechnen des entsprechenden bestimmten Integrals (natürlich unter Verwendung der parametrischen Form der Ellipse und der Formel für die Fläche des Bereichs in parametrischer Form):
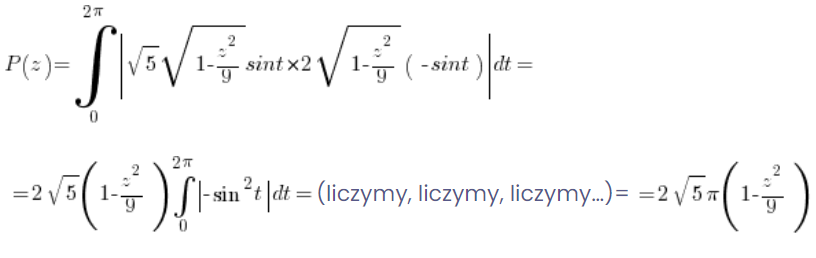
5. Berechnen wir das Volumen des Körpers mit den Flächen der Schnitte
Jetzt kommt der knifflige Teil. Das Volumen des Körpers entspricht – das klingt etwas komisch – der “Summe” (also dem Integral) aller Schnitte, was im Allgemeinen:
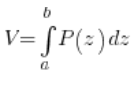
wobei 
die Funktion der Schnittflächen des Körpers mit einer Ebene senkrecht zur OZ-Achse ist, und ‘a’ und ‘b’ die Grenzen sind, innerhalb derer sich ‘z’ ändert.
Also bei uns:
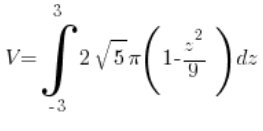= (rechnen, rechnen, rechnen…) = 
Das stimmt mit der allgemeinen Formel für das Ellipsoid überein (
).
ENDE
Es ist wichtig, sich dieses allgemeine Schema zu merken, und vor allem, dass das Volumen komplizierter, nicht-rotierender Körper durch das Integrieren der Funktion ihrer Schnittflächen berechnet werden kann.
Suchen Sie nach Mathe-Nachhilfe für das Universitätsniveau oder die Oberstufe? Oder benötigen Sie vielleicht einen Kurs, der Sie auf das Abitur vorbereitet?
Wir sind das Team von eTrapez. Wir unterrichten Mathematik auf eine klare, einfache und sehr detaillierte Weise - wir erreichen sogar diejenigen, die sich am meisten gegen das Lernen sträuben.
Wir haben Kurse in Videoform erstellt, die in einer verständlichen Sprache erklärt sind, zum Herunterladen auf Computer, Tablet oder Handy. Sie starten die Aufnahme, schauen und hören zu, als wären Sie bei der Nachhilfe. Zu jeder Tages- und Nachtzeit.
