The Volume of an Ellipsoid (But Not a Rotational One, Just a Wild Type) Calculated by a Definite Integral
Krystian Karczyński
Founder and General Manager of eTrapez.
Graduate of Mathematics at Poznan University of Technology. Mathematics tutor with many years of experience. Creator of the first eTrapez Courses, which have gained immense popularity among students nationwide.
He lives in Szczecin, Poland. He enjoys walks in the woods, beaches and kayaking.
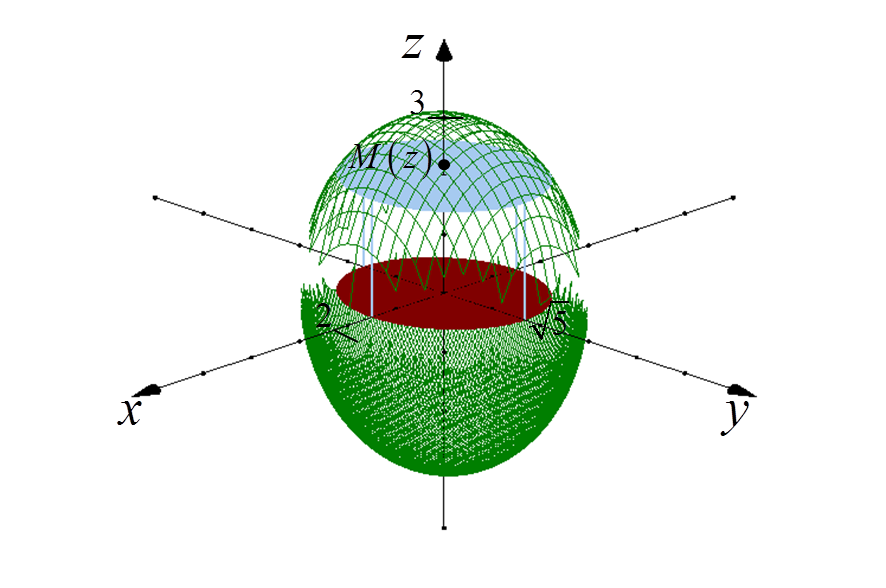
Let’s say we need to calculate the volume of an ellipsoid:
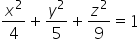
This ellipsoid intersects the x, y, z axes at coordinates 2, 
and 3, respectively (the general equation of the ellipsoid is: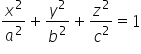 
, where a, b, c are the coordinates of the intersections).
This is not a rotational ellipsoid, not formed by rotating any curve around any axis, so we can’t use the standard formula for the volume of a rotational solid:
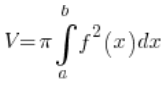
We need to figure out another way.
1. Choose any point M(z) at the center of the ellipsoid and on the OZ axis.
A plane passing through this point and perpendicular to the OZ axis “cuts” out a certain ellipse from the ellipsoid:
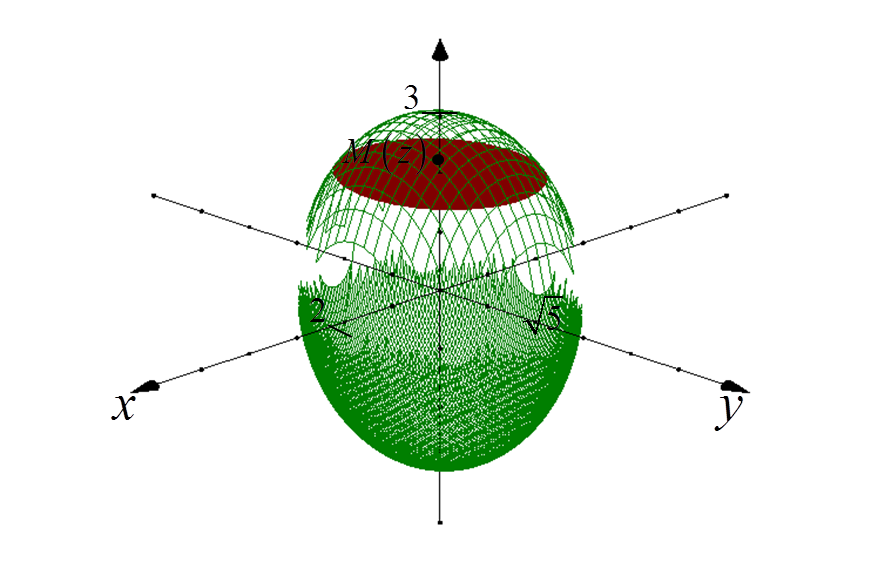
2. Determine the equation of the “cut-out” ellipse projection on the XY plane
We determine the equation of this ellipse, for a fixed ‘z’ (treating ‘z’ as a constant) from the general equation of the ellipsoid:
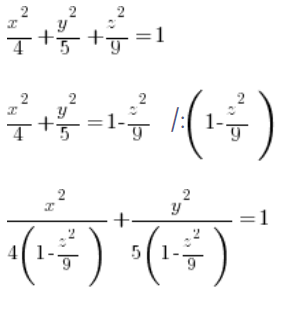
You can see that our ‘a’ and ‘b’ from the general equation of the ellipsoid (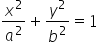
) are:
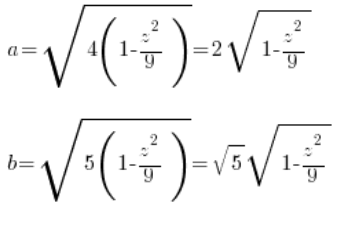
4. Calculate the area of this section as a function of ‘z’
The area of this ellipse depends on the chosen point ‘z’, so it will be a function of ‘z’. We can calculate it either using the ready formula for the area of an ellipse (
):
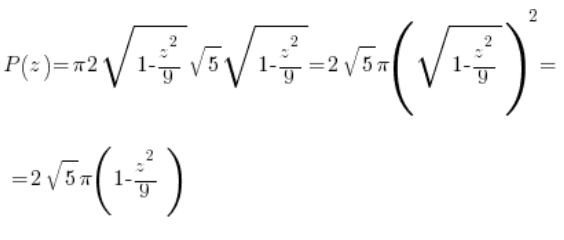
Or by laboriously calculating the appropriate definite integral (using, of course, the parametric form of the ellipse and the formula for the area of a region in parametric form):
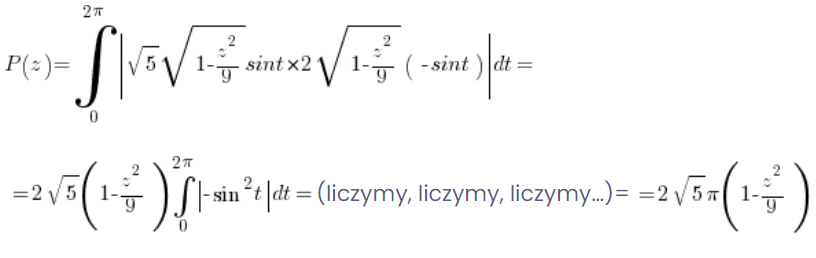
5. Calculate the volume of the solid using the cross-sectional areas
Now comes the tricky part. The volume of the solid is equal to – this sounds a bit awkward – the “sum” (i.e., the integral) of all the cross-sections, which in general is:
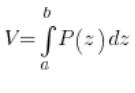
where 
is the function of the cross-sectional areas of the solid with a plane perpendicular to the OZ axis, and ‘a’ and ‘b’ are the bounds within which ‘z’ varies.
So for us:
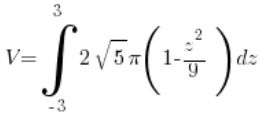= (calculate, calculate, calculate…) = 
This matches the general formula for the ellipsoid (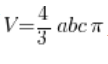
).
THE END
It’s worth remembering this general scheme, and most importantly, that the volume of more complex, non-rotational solids can be calculated by integrating the function of their cross-sectional areas.
Are you looking for college or high school math tutoring? Or maybe you need a course that will prepare you for the final exam?
We are "eTrapez" team. We teach mathematics in a clear, simple and very precise way - we will reach even the most knowledge-resistant students.
We have created video courses translated in an easy, understandable language, which can be downloaded to your computer, tablet or phone. You turn on the video, watch and listen, just like during private lessons. At any time of the day or night.
