Stetigkeit einer Funktion an einem Punkt
Wie wir alle wissen (zumindest aus meinem Kurs über Grenzwerte), ist die Funktion ![]() an dem Punkt
an dem Punkt ![]() stetig, wenn:
stetig, wenn:
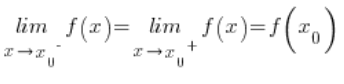
Das heißt, wenn der linksseitige Grenzwert dieser Funktion an diesem Punkt gleich dem rechtsseitigen Grenzwert dieser Funktion an diesem Punkt gleich dem Funktionswert an diesem Punkt ist.
Wenn eine dieser Gleichungen nicht erfüllt ist, ist die Funktion ![]() nicht stetig an dem Punkt
nicht stetig an dem Punkt ![]() , und der Punkt wird als Unstetigkeitsstelle bezeichnet.
, und der Punkt wird als Unstetigkeitsstelle bezeichnet.
In dieser Namensgebung können wir einen Schritt weiter gehen und die Unstetigkeitsstellen voneinander unterscheiden. Wir machen das so:
Unstetigkeitsstellen erster Art
Der Punkt ![]() wird als Unstetigkeitsstelle erster Art bezeichnet, wenn die Grenzwerte
wird als Unstetigkeitsstelle erster Art bezeichnet, wenn die Grenzwerte 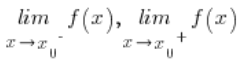 endlich sind (das heißt, einfach Zahlen sind).
endlich sind (das heißt, einfach Zahlen sind).
Zusätzlich, wenn diese Grenzwerte gleich sind, dann wird die Unstetigkeitsstelle erster Art als hebbar bezeichnet.
Unstetigkeitsstellen zweiter Art
Der Punkt ![]() wird als Unstetigkeitsstelle zweiter Art bezeichnet, wenn einer der Grenzwerte
wird als Unstetigkeitsstelle zweiter Art bezeichnet, wenn einer der Grenzwerte 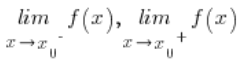 nicht endlich ist (das heißt, einfach gleich plus oder minus unendlich ist).
nicht endlich ist (das heißt, einfach gleich plus oder minus unendlich ist).
Beispiel 1
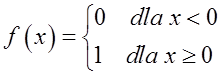
Diese Funktion hat an der Stelle ![]() eine Unstetigkeitsstelle (weil der linksseitige Grenzwert an dieser Stelle 0 und der rechtsseitige Grenzwert 1 ist). Es ist eine Unstetigkeitsstelle erster Art, weil die linksseitigen und rechtsseitigen Grenzwerte an dieser Stelle endlich sind (0 und 1). Es ist keine hebbare Unstetigkeitsstelle erster Art, weil die Grenzwerte nicht gleich sind.
eine Unstetigkeitsstelle (weil der linksseitige Grenzwert an dieser Stelle 0 und der rechtsseitige Grenzwert 1 ist). Es ist eine Unstetigkeitsstelle erster Art, weil die linksseitigen und rechtsseitigen Grenzwerte an dieser Stelle endlich sind (0 und 1). Es ist keine hebbare Unstetigkeitsstelle erster Art, weil die Grenzwerte nicht gleich sind.
Beispiel 2
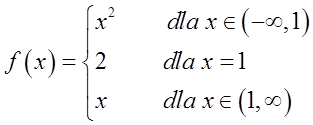
Diese Funktion hat an der Stelle ![]() eine Unstetigkeitsstelle (weil die linksseitigen und rechtsseitigen Grenzwerte an dieser Stelle nicht gleich dem Funktionswert an dieser Stelle sind). Es ist eine Unstetigkeitsstelle erster Art, weil die linksseitigen und rechtsseitigen Grenzwerte endlich sind (und gleich 1). Es ist eine hebbare Unstetigkeitsstelle erster Art, weil die linksseitigen und rechtsseitigen Grenzwerte gleich sind.
eine Unstetigkeitsstelle (weil die linksseitigen und rechtsseitigen Grenzwerte an dieser Stelle nicht gleich dem Funktionswert an dieser Stelle sind). Es ist eine Unstetigkeitsstelle erster Art, weil die linksseitigen und rechtsseitigen Grenzwerte endlich sind (und gleich 1). Es ist eine hebbare Unstetigkeitsstelle erster Art, weil die linksseitigen und rechtsseitigen Grenzwerte gleich sind.
Beispiel 3
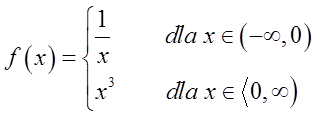
Diese Funktion hat an der Stelle ![]() eine Unstetigkeitsstelle (weil die linksseitigen und rechtsseitigen Grenzwerte an dieser Stelle nicht gleich sind). Es ist eine Unstetigkeitsstelle zweiter Art, weil der linksseitige Grenzwert an dieser Stelle
eine Unstetigkeitsstelle (weil die linksseitigen und rechtsseitigen Grenzwerte an dieser Stelle nicht gleich sind). Es ist eine Unstetigkeitsstelle zweiter Art, weil der linksseitige Grenzwert an dieser Stelle ![]() ist.
ist.


