fbpx

Szeregi

Categories

Pozostałe kategorie:
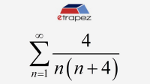
Miniaturka do video o obliczaniu sumu szeregów z definicji

Suma szeregu liczona z definicji (VIDEO)

05 października 2012 / Krystian Karczyński

Na filmiku poniżej pokazuję krok po kroku, jak obliczyć sumę szeregu z definicji. Sztuczka zastosowana w filmiku jest bardzo typowa, ale sam przykład trochę trudniejszy niż na ogół.

Czytaj dalej
Szereg o wyrazach niedodatnich - ikona

Szereg o Wyrazach Niedodatnich? – Żaden Problem z Kryteriami Abela i Dirichleta

08 maja 2012 / Krystian Karczyński

W ostatnim poście na blogu pokazałem kilka dodatkowych kryteriów, których użyć można do określenia zbieżności szeregów o wyrazach dodatnich. Czas więc na lekkie wzmocnienie artylerii na odcinku szeregów o wyrazach już niekoniecznie dodatnich. Dużym problemem studentów jest to, że mechanicznie próbują stosować kryterium d'Alemberta, porównawcze, całkowe itd. w przypadkach, w których tych kryteriów stosować nie można już na starcie...

Czytaj dalej

Wykorzystaj Podobieństwa Między Całkami a Szeregami

10 maja 2012 / Krystian Karczyński

Obliczanie całki oznaczonej (no i niewłaściwej także) to - jak możesz sprawdzić wgłębiając się trochę w definicję tej całki - właściwie obliczanie pewnego szeregu. Same całkowanie właściwie to tak naprawdę sumowanie, tyle, że wielkości nieskończenie małych. A suma to przecież szereg. Kryterium całkowe zbieżności szeregów (mając do określenie zbieżność szeregu liczymy odpowiadającą mu całkę i sprawdzamy jej zbieżność) już znasz. Jest to jednak tylko jeden element z dłuższej listy analogii i podobieństw. W tym poście opiszę 4 kryteria zbieżności, które znasz (no przynajmniej jedno na pewno znasz) z szeregów, w zupełnie identyczny sposób zastosowane do całek.

Czytaj dalej
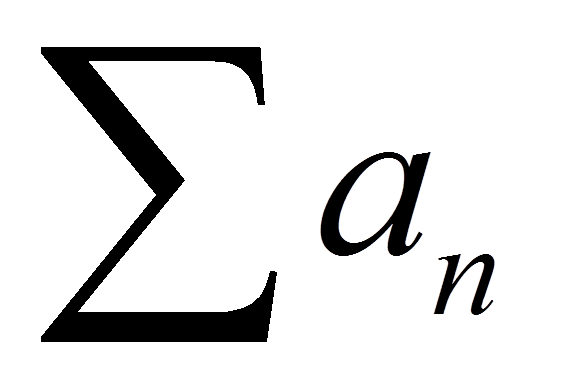
Szereg

5 Kryteriów Zbieżności Szeregów

30 kwietnia 2012 / Krystian Karczyński

Jest sobie szereg SUMA a(n) o wyrazach nieujemnych. Mamy sprawdzić, czy jest on zbieżny. Mamy do dyspozycji albo definicję (katorga), albo kryteria (spacer po łące). Skupmy się na kryteriach. W moim Kursie Szeregów pokazałem najczęściej używane: d'Alemberta, Cauchy'ego, porównawcze, całkowe. Oczywiście nie oznacza to, że lista możliwych kryteriów zbieżności została w ten sposób wyczerpana. W tym poście zajmę się pozostałymi, wprowadzanymi w podręcznikach i przez niektórych profesorów....

Czytaj dalej
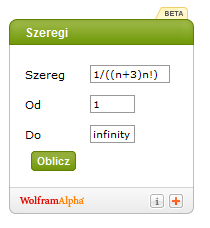
Obrazek kalkulatora do szeregów

Kalkulator Do Szeregów

13 stycznia 2012 / Krystian Karczyński

Przedstawiam kolejny kalkulator Wolphrama, przerobiony lekko przeze mnie. Ta zabawka poniżej służy do obliczania sumy szeregów (nie tylko liczbowych, ale i funkcyjnych!).

Czytaj dalej
Kurs Szeregi

Mój nowy Kurs Szeregi już gotowy

02 stycznia 2012 / Krystian Karczyński

Miło mi powiadomić, że skończyłem pracę nad Kursem Szeregów i jest już dostępny w sprzedaży: Kurs Szeregi. Kurs zawiera prawie 14 godzin nagrań video, zadania domowe, wzory i tak dalej, jak zawsze. Przerobiłem w nim szeregi -  od obliczania sum liczbowych z definicji po szeregi Fouriera. Przykładowe fragmenty Kursu możecie znaleźć w postach poniżej.

Czytaj dalej

Fragment Kursu Szeregów – kryterium d’Alemberta (“premiera” jutro) (VIDEO)

30 grudnia 2011 / Krystian Karczyński

Przedstawiam kolejny fragment mojego Kursu Szeregów (Kurs powinien ukazać się w sprzedaży już jutro), a w nim najbardziej chyba popularne kryterium zbieżności szeregu - kryterium d'Alamberta.

Czytaj dalej

Szeregi, Achilles i żółw (fragment nowego Kursu Szeregów) – (VIDEO)

07 listopada 2011 / Krystian Karczyński

Ciężko ruszyć z szeregami, jeśli się nie wie, co to szereg :) Przedstawiam więc krótkie wprowadzenie video + klasyczny paradoks z Achillesem i żółwiem. Sprawiał on spore trudności największym myślicielom przez całe stulecia, a jest bardzo prosty do rozpracowania przy użyciu matematyki i szeregów właśnie.

Czytaj dalej

Najnowsze komentarze na Blogu

No tak, w racja. Można rozwiązać przed podstawienie, dzięki za wskazanie :)

Krystian Karczyński

w poście:

"Zakazane Wzory Na Całki Nieoznaczone"

Moim zdaniem poprawne obliczenie całki nr 5 jest takie jak poniżej. Funkcję 3^x przedstawiamy jako (e^ln 3)^x i dalej (e^x) ^ln 3. Stosujemy podstawienie e^x=t, dx=dt/t i obliczamy całkę f-cji t^(ln 3 - 1) względem t, otrzymując t^(ln 3)/ln 3 + C. Po przejściu na zmienną x mamy wynik 3^x/ln 3 + C. Pozdrawiam.

Mirosław

w poście:

"Zakazane Wzory Na Całki Nieoznaczone"

Mała awaria przy testowaniu mobilnej. Przepraszamy.

Krystian Karczyński

w poście:

"O nas"

Witam mam pytanie o co chodzi że na komputerze kurs z matematyki podstawowej jest za 59 zł a w aplikacji google za 39 po czym z rabatem 29? W dodatku aplikacja jest w języku angielskim. Czy jeśli zakupie kurs w aplikacji bo jest taniej to bedzie on w języku polskim?

user-1272511690199847

w poście:

"O nas"

Dzień dobry, ten Kurs zaczęliśmy nagrywać w 2018 roku i nagrywaliśmy przez kilka lat, ale rok temu dokładnie go remontowaliśmy, żeby przystosować do wymogów nowej matury w 2023 roku. Zawiera najnowsze, uaktualnione rok temu informacje. Przepraszam za ten niedziałający filmik demonstracyjny, poprawiłem link i już powinno działać. Oczywiście w Kursie wszystko jest w porządku, do tej pory kupiło go ponad 9000 osób :)

Krystian Karczyński

w poście:

"O nas"

Najnowsze Kursy

Zobacz wszystkie Kursy eTrapez