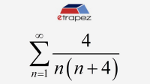
Suma szeregu liczona z definicji (VIDEO)
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Na filmiku poniżej pokazuję krok po kroku, jak obliczyć sumę szeregu z definicji. Sztuczka zastosowana w filmiku jest bardzo typowa, ale sam przykład trochę trudniejszy niż na ogół.
Zapraszam:
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.










Witam, czy w zad dom w lekcji 1 w pkcie b) nie jest błąd? Jest to szereg ((od n=1) 1/(n+1)(n+2)).Mi wychodzi 1/2, w odp jest 1.Nie wiem co mogło być źle. Z góry dziękuje za pomoc.pozdrawiam
Mi również wychodzi 1/2, również według mnie jest tam błąd.
Mi również wyszło 1/2.
Witam, czy mógłby Pan podpowiedzieć mi jak rozwiązać przykład: Znaleźć sumy częściowe podanych szeregów i następnie zbadać ich zbieżność Suma od n=2 do n=nieskończoność (n-1)/n!
mam prośbę czy mógłbyś pokazać mi jak liczyć sumę w takim przypadku jak w pdp e) i f) z tego samego zestawu w zadaniach domowych . mamy tam szereg postaci 4^n + 5^n/6^n . kompletnie nie wiem od czego zacząć .Twój projekt uważam za znakomity. Wiele razy mi pomógł dzięki.
Jasne.
Na początku warto rozbić wyrażenie pod szeregiem na dwa ułamki:
\sum\limits_{n=1}^{\infty }{\frac{{{4}^{n}}+{{5}^{n}}}{{{6}^{n}}}}=\sum\limits_{n=1}^{\infty }{\left( \frac{{{4}^{n}}}{{{6}^{n}}}+\frac{{{5}^{n}}}{{{6}^{n}}} \right)}=\sum\limits_{n=1}^{\infty }{\left( {{\left( \frac{4}{6} \right)}^{n}}+{{\left( \frac{5}{6} \right)}^{n}} \right)}=\sum\limits_{n=1}^{\infty }{\left( {{\left( \frac{2}{3} \right)}^{n}}+{{\left( \frac{5}{6} \right)}^{n}} \right)}
Potem zapisać ciąg sum częściowych (tak jak to pokazuję na przykładzie w Kursie):
{{S}_{1}}={{\left( \frac{2}{3} \right)}^{1}}+{{\left( \frac{5}{6} \right)}^{1}}
{{S}_{2}}={{\left( \frac{2}{3} \right)}^{1}}+{{\left( \frac{5}{6} \right)}^{1}}+{{\left( \frac{2}{3} \right)}^{2}}+{{\left( \frac{5}{6} \right)}^{2}}
{{S}_{3}}={{\left( \frac{2}{3} \right)}^{1}}+{{\left( \frac{5}{6} \right)}^{1}}+{{\left( \frac{2}{3} \right)}^{2}}+{{\left( \frac{5}{6} \right)}^{2}}+{{\left( \frac{2}{3} \right)}^{3}}+{{\left( \frac{5}{6} \right)}^{3}}
\ldots
{{S}_{n}}={{\left( \frac{2}{3} \right)}^{1}}+{{\left( \frac{5}{6} \right)}^{1}}+{{\left( \frac{2}{3} \right)}^{2}}+{{\left( \frac{5}{6} \right)}^{2}}+{{\left( \frac{2}{3} \right)}^{3}}+{{\left( \frac{5}{6} \right)}^{3}}+\ldots +{{\left( \frac{2}{3} \right)}^{n}}+{{\left( \frac{5}{6} \right)}^{n}}
Teraz policzyć jego granicę:
\underset{n\to \infty }{\mathop{lim }}\left[ {{\left( \frac{2}{3} \right)}^{1}}+{{\left( \frac{5}{6} \right)}^{1}}+{{\left( \frac{2}{3} \right)}^{2}}+{{\left( \frac{5}{6} \right)}^{2}}+{{\left( \frac{2}{3} \right)}^{3}}+{{\left( \frac{5}{6} \right)}^{3}}+\ldots +{{\left( \frac{2}{3} \right)}^{n}}+{{\left( \frac{5}{6} \right)}^{n}} \right]
Po przestawieniu kolejności składników dodawania w tym ciągu…
\underset{n\to \infty }{\mathop{lim }}\left[ {{\left( \frac{2}{3} \right)}^{1}}+{{\left( \frac{2}{3} \right)}^{2}}+{{\left( \frac{2}{3} \right)}^{3}}+\ldots +{{\left( \frac{2}{3} \right)}^{n}}+{{\left( \frac{5}{6} \right)}^{1}}+{{\left( \frac{5}{6} \right)}^{2}}+{{\left( \frac{5}{6} \right)}^{3}}+\ldots +{{\left( \frac{5}{6} \right)}^{n}} \right]
Widzimy, że składa się on z sumy dwóch szeregów geometrycznych znanych ze szkoły średniej, tzn. szeregów geometrycznych o ilorazach q = 2/3i q=5/6. Są to szeregi zbieżne, ponieważ |q|<1. Zatem do obliczenia tych sum można zastosować wzór ze średniej S=\frac{{{a}_{1}}}{1-q}:
{{S}_{1}}=\underset{n\to \infty }{\mathop{lim }}\left[ {{\left( \frac{2}{3} \right)}^{1}}+{{\left( \frac{2}{3} \right)}^{2}}+{{\left( \frac{2}{3} \right)}^{3}}+\ldots +{{\left( \frac{2}{3} \right)}^{n}} \right]=\frac{\tfrac{2}{3}}{1-\tfrac{2}{3}}=\frac{\tfrac{2}{3}}{\tfrac{1}{3}}=\frac{2}{3}\cdot \frac{3}{1}=2
{{S}_{2}}=\underset{n\to \infty }{\mathop{lim }}\left[ {{\left( \frac{5}{6} \right)}^{1}}+{{\left( \frac{5}{6} \right)}^{2}}+{{\left( \frac{5}{6} \right)}^{3}}+\ldots +{{\left( \frac{5}{6} \right)}^{n}} \right]=\frac{\tfrac{5}{6}}{1-\tfrac{5}{6}}=\frac{\tfrac{5}{6}}{\tfrac{1}{6}}=\frac{5}{6}\cdot \frac{6}{1}=5
Zatem granicą ciągu sum częściowych będzie:
\underset{n\to \infty }{\mathop{lim }}\left[ {{\left( \frac{2}{3} \right)}^{1}}+{{\left( \frac{2}{3} \right)}^{2}}+{{\left( \frac{2}{3} \right)}^{3}}+\ldots +{{\left( \frac{2}{3} \right)}^{n}}+{{\left( \frac{5}{6} \right)}^{1}}+{{\left( \frac{5}{6} \right)}^{2}}+{{\left( \frac{5}{6} \right)}^{3}}+\ldots +{{\left( \frac{5}{6} \right)}^{n}} \right]=2+5=7
Witam . Prosił bym o pomoc w policzeniu tych szeregów zrobiłem pare ale nie jestem pewien czy dobrze (wszystko od jedynki oprocz a)) :
kryterium Cauchy’ego
a) “od 2” 1/(lnn)^n
b) ((3n+1)/(n+2))^n
c) (3/n)^n
oraz kryterium d’Alamberta.
a)1/n!
b)n^n/n1
c)(3n)!/(n^3n)
Z góry bardzo dziekuje !!!