Co Robić, Żeby Uczyć Się Szybciej? (Wskazówka Dnia) – (VIDEO)
Krystian Karczyński
8 lutego 2012
7 komentarzy
W filmiku przedstawiam bardzo pewną i prostą metodę na to, żeby uczyć się szybciej.
Nowy Wykład na blogu – Całki Oznaczone
Krystian Karczyński
6 lutego 2012
5 komentarzy
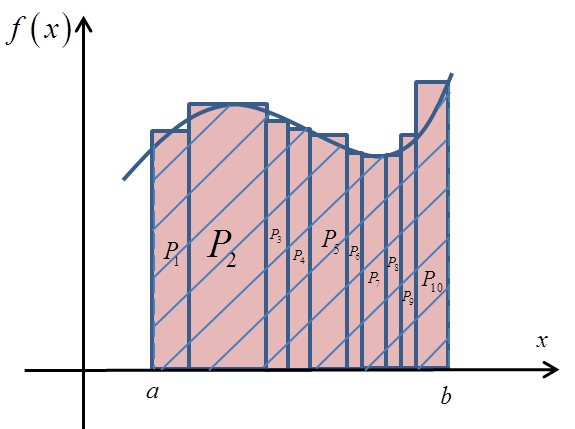
Do moich Wykładów na blogu (na prawym pasku) dodałem artykuł poświęcony całce oznaczonej: Definicja całki oznaczonej.
Mam nadzieję, że pomoże Wam zrozumieć tą definicję, bo nie jest szczególnie trudna (jak się już przekroczy pewną trudność w zrozumieniu, jak można coś sumować w nieskończoność i mieć skończoną wartość tego sumowania).
Granice z pierwiastkami trzeciego stopnia (czyżby mnożenie przez sprzężenie?)
Krystian Karczyński
1 lutego 2012
31 komentarzy
Mając daną do policzenia granicę, do której jakoś zamieszane było jakieś odejmowanie z pierwiastkiem (i której nie dało się obliczyć prościej, rzecz jasna), czyli: „COŚ – pierwiastek z czegoś”, „pierwiastek z czegoś – COŚ” lub też „pierwiastek z czegoś – pierwiastek z czegoś” stosowaliśmy sztuczkę, którą ja nazywam – „mnożenie przez sprzężenie”.
Po prostu mnożyliśmy to wyrażenie przez jego odpowiednik ze znakiem plus, a właściwie przez ułamek, w którym był ten odpowiednik w liczniku i mianowniku.
Co zrobić gdy pierwiastki są trzeciego stopnia?
eTrapez Uporządkowany – Mapa Treści
Krystian Karczyński
30 stycznia 2012
41 komentarzy
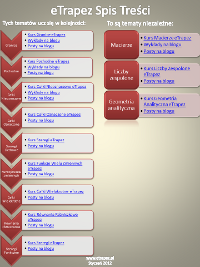
Mamy styczeń 2012 i na eTrapezie uzbierało się już 11 Kursów (EDYCJA: na sierpień 2012 jest to już 12 Kursów, EDYCJA: na styczeń 2013 jest to już 13 Kursów), a także wiele wykładów i postów na blogu. Dostaję sporo emaili z prośbą o jakieś usystematyzowanie tego wszystkiego.
Ludzie pytają, od jakich Kursów należy zacząć, co już trzeba umieć, żeby zacząć X i co należy robić po przerobieniu Y. Dlatego poniżej wklejam „mapkę” treści mojego serwisu (tzn. Kursów + blogu).
Granice ciągu z sumą kwadratów lub sumą sześcianów
Krystian Karczyński
27 stycznia 2012
Brak komentarzy
W granicach ciągów bywa czasami tak, że wyrażenie zawiera sumę kwadratów lub też sześcianów kolejnych liczb naturalnych. Co wtedy?
Odpowiedź jest prosta: wzory na sumę kwadratów i na sumę sześcianów kolejnych liczb naturalnych. Szły one tak…
Wirtualny nauczyciel AI działający w przeglądarce internetowej.