Kategoria: Całki oznaczone

Liczenie całek oznaczonych z definicji to niełatwa sztuka. Po pierwsze trzeba tą definicję rozumieć. Tym już się zająłem w poprzednich wykładach. Po drugie, trzeba umieć tą definicję w praktyce zastosować.

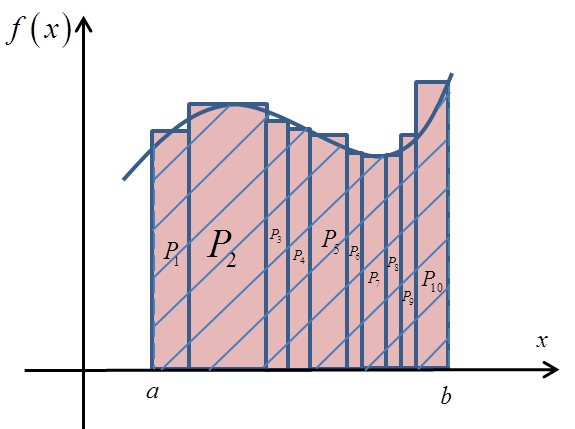
Tutaj właśnie z pomocą idą odkryte (lub wymyślone – zależnie od filozofii matematyki, jaką wyznajesz 🙂 ) jakieś ponad 100 lat temu sumy Darboux (to ten Pan na zdjęciu).

Odkryj sam, jak bardzo porządkują one chaos „czystej” definicji i jej dowolności.

Powiedzmy, że do policzenia mamy objętość elipsoidy: {x^2}/4+{y^2}/5+{z^2}/9=1. Jest to elipsoida, która przecina osie x,y,z we współrzędnych odpowiednio: 2, pierw{5} i 3.

Nie jest to elipsoida obrotowa, nie powstaje przez obrót jakiejkolwiek krzywej wokół jakiejkolwiek osi, nie poradzimy sobie standardowym wzorem na objętość bryły obrotowej. Trzeba kombinować inaczej.

Liczenie całek oznaczonych z DEFINICJI (nie korzystając z całek nieoznaczony i wzory Newtona-Leibnitz’a) jest ciężkie, jak wszyscy wiemy.

Zrobiłem więc na ten temat mały „Wykład”, w którym kroczek po kroczku, powoli wyjaśniam, co i jak. Tym razem pokazuję, jak to robić, na 3 konkretnych przykładach. Myślę, że po uważnym przejrzeniu Wykładu sam bez trudu załapiesz metodę.

Powodzenia z całkami oznaczonymi i ich definicjami na studiach!

Do moich Wykładów na blogu (na prawym pasku) dodałem artykuł poświęcony całce oznaczonej: Definicja całki oznaczonej.

Mam nadzieję, że pomoże Wam zrozumieć tą definicję, bo nie jest szczególnie trudna (jak się już przekroczy pewną trudność w zrozumieniu, jak można coś sumować w nieskończoność i mieć skończoną wartość tego sumowania).