 Całkowanie a liczenie szeregów – tak różne, a tak podobne
Całkowanie a liczenie szeregów – tak różne, a tak podobne
Obliczanie całki oznaczonej (no i niewłaściwej także) to – jak możesz sprawdzić wgłębiając się trochę w definicję tej całki – właściwie obliczanie pewnego szeregu.
Same całkowanie właściwie to tak naprawdę sumowanie, tyle, że wielkości nieskończenie małych. A suma to przecież szereg.
Trudno więc, żeby pomiędzy całką \int\limits_{a}^{\infty }{f\left( x \right)dx}, a szeregiem \sum\limits_{n=a}^{\infty }{{{a}_{n}}} nie było wielu analogii.
Kryterium całkowe zbieżności szeregów (mając do określenie zbieżność szeregu liczymy odpowiadającą mu całkę i sprawdzamy jej zbieżność) już znasz. Jest to jednak tylko jeden element z dłuższej listy analogii i podobieństw.
Dzięki nim określisz w wielu przypadkach zbieżność (lub nie) całki niewłaściwej, bez konieczności obliczania jej od deski do deski. Ułatwia to sprawę, a czasami nawet nie ułatwia, ale w ogóle umożliwia – bo jak już wiesz liczenie całek to często sprawa bardzo trudna.
W tym poście opiszę 4 kryteria zbieżności, które znasz (no przynajmniej jedno na pewno znasz) z szeregów, w zupełnie identyczny sposób zastosowane do całek.
-
Kryterium porównawcze
Tak, tak, to nasz stary dobry znajomy z szeregów. Znany i popularny, choć nie bardzo lubiany przez studentów za brak sztywno określonego schematu postępowania.
Przypomnę: chodziło tam o to, że szukałem ciągów ograniczających wyraz szeregu od dołu lub od góry (w zależności, czy wykazywałem zbieżność, czy rozbieżność) i takich, żeby szeregi z tych ciągów były rozbieżne lub zbieżne (znowu w zależności od tego, co chciałem pokazać).
Wszystko to pokazałem w moim Kursie Szeregów.
No i spójrz teraz na kryterium porównawcze całek niewłaściwych:
Kryterium porównawcze zbieżności całek niewłaściwych
- Jeśli funkcja f\left( x \right) jest funkcją dodatnią od pewnego x(dla x\ge {{x}_{0}}, gdzie {{x}_{0}} oznacza jakąś stałą) i dla tych x zachodzi nierówność f\left( x \right)\le g\left( x \right), to ze zbieżności całki \int\limits_{{{x}_{0}}}^{\infty }{g\left( x \right)dx} wynika zbieżność całki \int\limits_{{{x}_{0}}}^{\infty }{f\left( x \right)dx}
- Jeśli funkcja f\left( x \right) jest funkcją dodatnią od pewnego x(dla x\ge {{x}_{0}}, gdzie {{x}_{0}} oznacza jakąś stałą) i dla tych x zachodzi nierówność f\left( x \right)\ge g\left( x \right), to z rozbieżności całki \int\limits_{{{x}_{0}}}^{\infty }{g\left( x \right)dx} wynika rozbieżność całki \int\limits_{{{x}_{0}}}^{\infty }{f\left( x \right)dx}
Jest to właściwie zdublowane kryterium w stosunku do tego z szeregów, a i metoda postępowania taka sama.
Przykład 1
Zbadaj zbieżność całki \int\limits_{1}^{\infty }{\frac{1}{{{x}^{2}}+x}dx}
Alternatywą do męczącego obliczania wprost tej całki i sprawdzaniu na końcu, czy wyjdzie stała, czy nieskończoność (pokazałem jak to się robi w moim Kursie z całkami niewłaściwymi) jest zastosowanie kryterium porównawczego.
Zupełnie analogicznie, jak w szeregach patrząc na funkcję podcałkową orientuję się, że będę szacował zbieżność, szukam więc jej oszacowania z góry:
\frac{1}{{{x}^{2}}+x}\leZmniejszając mianownik zwiększę całe wyrażenie, czyli:
\frac{1}{{{x}^{2}}+x}\le \frac{1}{{{x}^{2}}}– oczywiście dla x>1, a tylko takie bierzemy pod uwagę patrząc na granice całkowania
Całka \int\limits_{1}^{\infty }{\frac{1}{{{x}^{2}}}dx} jest oczywiście zbieżna, możemy to pokazać Panu Profesorowi obliczając ją w kilku ruchach (to już będzie elementarna, a nie wymierna) – jeśli w ogóle tego wymaga.
Czyli – na mocy kryterium porównawczego całek niewłaściwych – całka \int\limits_{1}^{\infty }{\frac{1}{{{x}^{2}}+x}dx} jest zbieżna.
Kolejne kryterium opisałem w moim poście parę dni temu, jako kryterium do szeregów. Świetnie jednak sprawdza się również dla całek niewłaściwych:
2. Kryterium ilorazowe
Kryterium ilorazowe zbieżności całek niewłaściwych
Jeśli mam dwie całki \int\limits_{{{x}_{0}}}^{\infty }{f\left( x \right)dx} i \int\limits_{{{x}_{0}}}^{\infty }{g\left( x \right)dx}, oraz istnieje granica:
\underset{x\to \infty }{\mathop{\lim }}\,\frac{f\left( x \right)}{g\left( x \right)}wtedy jeżeli:
- 0<\underset{x\to \infty }{\mathop{\lim }}\,\frac{f\left( x \right)}{g\left( x \right)}<\infty – obie całki są równocześnie albo zbieżne, albo rozbieżne
- \underset{x\to \infty }{\mathop{\lim }}\,\frac{f\left( x \right)}{g\left( x \right)}=0– ze zbieżności całki \int\limits_{{{x}_{0}}}^{\infty }{g\left( x \right)dx} wynika zbieżność całki \int\limits_{{{x}_{0}}}^{\infty }{f\left( x \right)dx}
- \underset{x\to \infty }{\mathop{\lim }}\,\frac{f\left( x \right)}{g\left( x \right)}=\infty – z rozbieżności całki \int\limits_{{{x}_{0}}}^{\infty }{g\left( x \right)dx} wynika rozbieżność całki \int\limits_{{{x}_{0}}}^{\infty }{f\left( x \right)dx}
Przykład 2
Zbadaj zbieżność całki \int\limits_{2}^{\infty }{\frac{x+3}{{{x}^{3}}+\sqrt{x}-1}dx}
Tutaj motanie się z liczeniem tej całki było by już zupełnie przykre (chociaż możliwe). Podejdźmy ją elegancko dobranym kryterium ilorazowym.
Mamy funkcję \frac{x+3}{{{x}^{3}}+\sqrt{x}-1}, trzeba ją podzielić przez odpowiednią funkcję. Największa potęga w liczniku to x, a w mianowniku x^3. Dzielę więc przez funkcję \frac{x}{{{x}^{3}}} i zobacz, jak fajnie uprości to nam temat:
\underset{x\to \infty }{\mathop{\lim }}\,\frac{\frac{x+3}{{{x}^{3}}+\sqrt{x}-1}}{\frac{x}{{{x}^{3}}}}=\underset{x\to \infty }{\mathop{\lim }}\,\frac{x+3}{{{x}^{3}}+\sqrt{x}-1}\cdot \frac{{{x}^{3}}}{x}=\underset{x\to \infty }{\mathop{\lim }}\,\frac{x+3}{x}\cdot \frac{{{x}^{3}}}{{{x}^{3}}+\sqrt{x}-1}=\underset{x\to \infty }{\mathop{\lim }}\,\left( 1+\frac{3}{x} \right)\cdot \frac{{{x}^{3}}}{{{x}^{3}}\left( 1+\frac{\sqrt{x}}{{{x}^{3}}}-\frac{1}{{{x}^{3}}} \right)}=1Czyli nasza granica z kryterium ilorazowego wyszła równa 1, zatem obie całki \int\limits_{2}^{\infty }{\frac{x+3}{{{x}^{3}}+\sqrt{x}-1}dx} i \int\limits_{2}^{\infty }{\frac{x}{{{x}^{3}}}dx} są albo równocześnie zbieżne, albo równocześnie rozbieżne.
A tak się oczywiście składa, że całka \int\limits_{2}^{\infty }{\frac{x}{{{x}^{3}}}dx}=\int\limits_{2}^{\infty }{\frac{1}{{{x}^{2}}}dx} jest zbieżna (co można znowu pokazać obliczając ją w kilku ruchach).
Zatem na mocy kryterium ilorazowego zbieżności całek niewłaściwych całka \int\limits_{2}^{\infty }{\frac{x+3}{{{x}^{3}}+\sqrt{x}-1}dx} jest zbieżna.
Uwaga!
Uważnie prześledź ten myk w tym przykładzie, jest on często dobierany przez profesorów. Nieznajomość jego oznacza Twoją śmierć na kolokwium (no chyba, że oszacujesz porównawczym, oczywiście), bo nie chodzi o to, żebyś całkę LICZYŁ, tak jak w standardowych przypadkach.
Funkcję podcałkową dzielisz przez największe potęgi w liczniku i mianowniku, a jak są pod pierwiastkiem, to też pod pierwiastkiem. Na przykład, żeby policzyć całkę \int\limits_{2}^{\infty }{\frac{\sqrt[3]{x}}{\sqrt{{{x}^{3}}-7}}dx} utworzyłbyś granicę: \underset{x\to \infty }{\mathop{\lim }}\,\frac{\frac{\sqrt[3]{x}}{\sqrt{{{x}^{3}}-7}}}{\frac{\sqrt[3]{x}}{\sqrt{{{x}^{3}}}}}
Kolejne kryteria nie wymagają tego, żeby funkcja podcałkowa była dodatnia. Ich odpowiedniki w szeregach wprowadziłem w ostatnim poście na blogu.
3. Kryterium Abela
Kryterium Abela zbieżności całek niewłaściwych
Jeśli funkcje f\left( x \right) i g\left( x \right) są określone w przedziale < a,\infty ), całka \int\limits_{a}^{\infty }{f\left( x \right)dx} jest zbieżna w tym przedziale, a funkcja g\left( x \right) jest monotoniczna i ograniczona w tym przedziale, wtedy całka:
\int\limits_{a}^{\infty }{f\left( x \right)g\left( x \right)dx}jest zbieżna.
4. Kryterium Dirichleta
Kryterium Dirichleta zbieżności całek niewłaściwych
Jeżeli:
- funkcja f\left( x \right) jest całkowalna w każdym przedziale \left\langle a,A \right\rangle dla A>a i całka \int\limits_{a}^{A}{f\left( x \right)dx} jest w nim ograniczona
- funkcja g\left( x \right) jest monotoniczna i zbieżna do zera, gdy x\to \infty
wtedy:
\int\limits_{a}^{\infty }{f\left( x \right)g\left( x \right)dx}
jest zbieżna.
Przykład 3
Zbadaj zbieżność całki \int\limits_{1}^{\infty }{\frac{\sin x}{\sqrt{x}}dx}
Jeśli ktoś chciałby liczyć tą całkę, to oczywiście powodzenia, ale o wiele lepiej przedstawić ją jako:
\int\limits_{1}^{\infty }{\frac{1}{\sqrt{x}}\sin xdx}Podchodzimy do kryterium Dirichleta, czyli pokazujemy, że całka \int\limits_{a}^{A}{\sin xdx} jest całkowalna i ograniczona – po prostu ją licząc:
\int\limits_{a}^{A}{\sin xdx}=\ldots \int{\sin xdx}=-\cos x+C \ldots =\left. \left[ -\cos x \right] \right|_{a}^{A} \ldots =\left. \left[ -\cos x \right] \right|_{a}^{A}=-\cos A-\left( -\cos a \right)=\cos a-\cos ACzyli funkcja \sin x jest całkowalna i ograniczona też, bo \cos a i \cos A nigdy nie „przekroczą” wartości -1 i 1, czyli na pewno:
-2\le \cos a-\cos A\le 2Dalej funkcja \frac{1}{\sqrt{x}} jest monotoniczna (malejąca) i \underset{x\to \infty }{\mathop{\lim }}\,\frac{1}{\sqrt{x}}=0.
Czyli założenia kryterium Dirichleta są spełnione. Zatem:
Na mocy kryterium Dirichleta całka \int\limits_{1}^{\infty }{\frac{\sin x}{\sqrt{x}}dx}jest zbieżna.
Ułatwia to wszystko pewne sprawy, prawda? 🙂

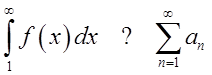
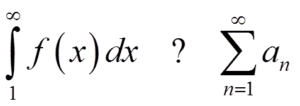 Całkowanie a liczenie szeregów – tak różne, a tak podobne
Całkowanie a liczenie szeregów – tak różne, a tak podobne
5 Komentarzy
kuba
a co jeśli granice w ogóle nie będą istnień w kryterium ilorazowym?
Magda
Dziękuję Krystian, w końcu zrozumiałam to nieszczęsne kryterium! Szybko, łatwo i zwięźle!
Michał
Brawo Krystian, swietna robota zarowno merytorycznie, jak i pod wzgledem prezentacji informacji, czytelnie i rzetelnie.
Pozdrawiam.
Przemysław Łabędź
Witam i przepraszam że tu zamieszczam ten post.
Jakieś 3 miesiące temu kolega kupił od pana 2 kursy całek wielokrotnych. I on już miał kolokwium a ja mam w sobotę i mam do pana proźbę o rozwiązanie lub nakierowanie w rozwiązaniu zadania bo u pana w kursie nie było jak rozwiązać takie zadanie:
Oblicz pole części powierzchni paraboloidy z=4-(x do kwadratu + y do kwadratu) wyciętej przez powierzchnie z=1, z=2. Chodzi o to że mam problem z wyznaczeniem obszaru całkowania jak wogóle wyznaczyć z niego do dalszej części zadania „x” i „y”. Rysunek narysowałem pana sposobem i jest czytelny i wyznaczyłem obszar całkowania ale nie wiem jak jest ograniczony chodzi o x i y.
Jak by pan mógł jak najszybciej mi pomóc.
Z góry dziękuje.
Piotr Michalak
Witam
Wiem, że komentarz dodany „troszkę” za późno ale z okazji sesji i mojego egzaminu z Analizy Matematycznej III za 6 godzin chciałbym zrobić coś związanego z tematem i nakierować na rozwiązanie tego zadania osoby, które tak jak ja będą szukać odpowiedzi na jest stronie.
Wstęp: Niemalże każde zadanie jest projektowane tak żeby było możliwe do rozwiązania metodami poznanymi przez na na ćwiczeniach oraz wykładach. Należy więc doszukiwać się jawnych wskazówek
Krok 1 wskazówki: Pole powierzchni płata S jest równe Całce po tym płacie z funkcji tożsamościowo równej 1. zdanie :Oblicz pole części powierzchni paraboloidy z=4-(x^2 + y^2) to jest swoiste: „Mój drogi Studencie teraz podaję Ci wzór funkcji (opis płata S)
A podanie warunków jakimi powierzchniami tniemy naszą paraboloidę jest wskazówką : „Mój drogi Studencie teraz podaję Ci jak będzie wyglądał rzut płata S na płaszczyznę OXY”
Krok 2 Korzystając z narzędzi jakie dostaliśmy w ręce od naszych Prowadzących i Wykładowców możemy teraz obliczyć taką całkę. Jak? Pierwszym pomysłem jaki przychodzi mi do głowy i zdaje się być najprostszy jest sprowadzenie tej całki do całki podwójnej. Wyznaczamy rzut płata S (podstawiając kolejno wartości z=1 i z=2 do równania z=4-(x^2+y^2) po chwili zastanowienia widać, że będzie to pierścień. Czyli całka sprowadza się do obliczenia całki podwójnej po pierścieniu z funkcji która prezentuje długość wektora normalnego do naszej powierzchni (po to została nam podana funkcja z=4-(x^2+y^2).
Krok 3. Obliczenie powyższej całki najlepiej zrobic poprzez podstawienie trygonometryczne ale to już inna bajka, którą na pewno znajdziecie w \internecie i najpewniej w kursie Pana Krystiana Karczyńskiego.
PM