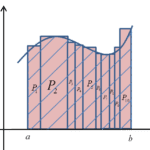
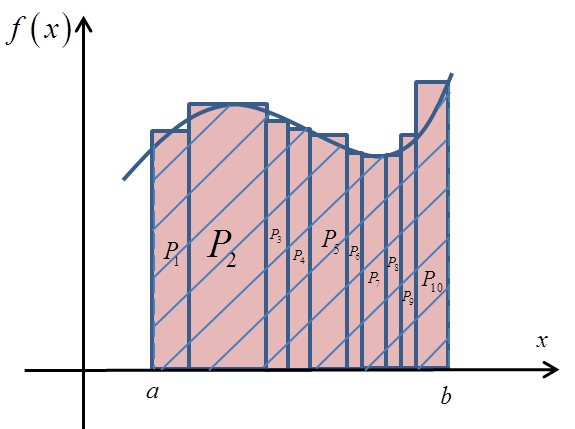
 Do moich Wykładów na blogu (na prawym pasku) dodałem artykuł poświęcony całce oznaczonej:
Do moich Wykładów na blogu (na prawym pasku) dodałem artykuł poświęcony całce oznaczonej:
Mam nadzieję, że pomoże Wam zrozumieć tą definicję, bo nie jest szczególnie trudna (jak się już przekroczy pewną trudność w zrozumieniu, jak można coś sumować w nieskończoność i mieć skończoną wartość tego sumowania).


5 Komentarzy
Monika
Czy mogłabym prosić o pomocw obliczeniu pola obszaru ograniczonego krzywymi?
y=arctgx, y=x, y=1 Nie wiem jak sobie z tym poradzić…
Krystian Karczyński
Wykres tego nie jest taki łatwy do narysowania, ale wyglądał by tak:
Kluczem do wszystkiego jest wiedza o tym, że arctgx0. Można – po prostu – to wiedzieć (wykres tgxleży nad prostą y=xdla x>0, czyli wykres arctgxbędzie leżał pod tą prostą. Można wziąć kalkulator i policzyć kilka wartości arctgxbardzo blisko zera.
Teraz:
Zadanie można zrobić klasycznie dzieląc obszar na dwie części. Wtedy trzeba policzyć jedną z granic całkowania przyrównując do siebie przecinające się tam krzywe (tak jak pokazuję w swoim Kursie):
arctgx=1
tg\left( arctgx \right)=tg1
x=tg1
No i tak niestety trzeba zostawić, jako pewną stałą.
Teraz liczę już obszar:
P=\int\limits_{0}^{1}{\left( x-arctgx \right)dx}+\int\limits_{1}^{tg1}{\left( 1-arctgx \right)dx}=\ldots
No i pomagając sobie kalkulatorkiem mam wynik:
\ldots =-\frac{1}{2}-ln cos 1
Czyli coś koło 0,12(w przybliżeniu).
Można też zrobić zadanie w stylu ninja, czyli całkując względem osi OY (trzeba wtedyprzekształcić funkcje x i arctgx na funkcje odwrotne, co jest akurat tutaj wyjątkowo proste):
P=\int\limits_{0}^{1}{\left( tgy-y \right)dy}=\ldots =-\frac{1}{2}-ln cos 1
A więcej o tym patencie znajdzie Pani w moim poście na blogu:
Całkowanie względem zmiennej y
Monika
bardzo dziękuję za pomoc 🙂
Przemysław
Pewnie to niezbyt właściwe miejsce na pozytywną opinię ale trudno. Chciałem napisać że dzięki Pana Kursom udało mi się zaliczyć Równania różniczkowe oraz analize matematyczną 3. Do całej tematyki podszedłem raczej bez podstaw kulały nawet całki nieoznaczone że o oznaczonych już nie wspomnę. Jednak spędziłem z Pana kursem bardzo wiele długich a czasem nawet bardzo dłuuugich godzin. Mogę z całą stanowczością stwierdzić że rozumiem równania różniczkowe i potrafię policzyć znaczną część całek wielokrotnych. Miałem do czynienia z Pana Kursami rok wcześniej , nauka szła błyskawicznie jednak wymienione przeze mnie kursy z calek wielokrotnych i RR mnie zaskoczyły. Prawie 5 h nagrania dla samych całek podwójnych .. Ponad dwie godz dla potrójnych.. Było bardzo ciężko i bardzo żmudnie, ale tak jak napisałem podwójny sukces i podwójna radość. Proponuję jednak dorzucić do kursu funkcji wielu zmiennych pochodne kierunkowe. Tego właśnie w kursie mi brakowalo i to odnalazlem tutaj na blogu. Pozdrawiam i dziękuje że robi Pan kawał dobrej roboty dla studentów.
Krystian Karczyński
Dzięki, gratuluję ciężkiej pracy i zaliczeń!