
Całki oznaczone liczone względem zmiennej y
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Całki oznaczone można liczyć zarówno względem zmiennej x, jaki i zmiennej y, a nawet powinno się, o ile jest wygodniej. Odgrywa to często dużą rolę w zastosowaniach całek, takich jak: obliczanie pól obszarów, długości łuków, objętości i pola powierzchni pól obrotowych. Często zresztą nie mamy nawet wyboru, bo w warunkach zadania jest określone, że krzywa kręci się wokół osi OY, a nie OX.
Jak to zrobić?
Przede wszystkim należy w tym celu wykonać rysunek i zaznaczyć na nim pole/długość łuku/objętość, które mamy policzyć. Bez tego nie ruszymy.
Po drugie należy wyznaczyć granice całkowania na osi OY (analogicznie, jak to się robiło na osi OX).
Teraz wystarczy już tylko krzywe ograniczające dane (na ogół) zmienną x wyznaczyć przy pomocy zmiennej y, np. mając krzywą ![]() , wyznaczamy z niej “x” i otrzymujemy w ten sposób dwie funkcje zmiennej y:
, wyznaczamy z niej “x” i otrzymujemy w ten sposób dwie funkcje zmiennej y: 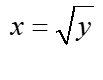 i
i 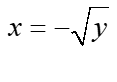 .
.
Potem tworzymy już tylko odpowiednią całkę z granicami całkowania na osi OY i funkcjami zmiennych y, np. w polu obszaru była by to:
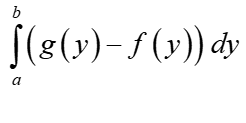
Jeszcze raz powtórzę, że podstawa to czytelny, duży wykres!
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.










Mam pytanie w sprawie zadania nr 3 z części drugiej, w którym należy obliczyć długość łuków krzywych (całki oznaczone). Otóż w odpowiedzi jest 14/3 a wynik wychodzi mi dwukrotnie większy. Coś pomyliłem, czy błąd w odpowiedzi?
Jest błąd w odpowiedzi, powinno być 28/3. Przepraszam!
y=x^2
x=x^(1/2) v x=-x^(1/2)
chyba nie do końca o to chodziło…
Tak, bez sensu wyszło, poprawiłem, dzięki wielkie za zwrócenie uwagi!
Na politechnice Wrocławskiej często zabraniają tak liczyć, karzą stosować osobne wzory na objętość i pole w okół osi OY
“każa” bo kazać, Robercie z politechniki Wrocławskiej 😛