القيم القصوى للدوال المحاضرة 7
الموضوع: الشرط الكافي لوجود قيمة قصوى للدالة (تغيير علامة المشتقة).
ملخص
كما اكتشفنا في المحاضرة السابقة، مجرد أن تكون المشتقة لدالة ما في نقطة معينة تساوي صفر لا يعني بالضرورة أن الدالة نفسها تحقق قيمة قصوى في هذه النقطة. هنا سنتحدث إذن عن الشروط التي تكفي لكي تحقق الدالة قيمة قصوى في نقطة ما.
الشروط الكافية لوجود القيم القصوى
لنفترض أنه في بيئة معينة حول نقطة x_0، الدالة f \left(x \right) لها مشتقة محدودة f' \left(x \right):
- إذا كانت قيم المشتقة للدالة على يسار x_0 موجبة، وعلى يمين x_0 سالبة – فإن الدالة تأخذ قيمة قصوى في نقطة x_0
- إذا كانت قيم المشتقة للدالة على يسار x_0 سالبة، وعلى يمين x_0 موجبة – فإن الدالة تأخذ قيمة دنيا في نقطة x_0
فعلا، بناءً على لمة الاحادية للدالة التي تم تقديمها في المحاضرة السابقة، إذا كانت المشتقة للدالة ![]() تأخذ قيم موجبة، يعني ذلك أن الدالة
تأخذ قيم موجبة، يعني ذلك أن الدالة ![]() في حالة تزايد. وإذا كانت المشتقة
في حالة تزايد. وإذا كانت المشتقة ![]() تأخذ قيم سالبة، يعني ذلك أن الدالة
تأخذ قيم سالبة، يعني ذلك أن الدالة ![]() في حالة تناقص.
في حالة تناقص.
إذا كانت المشتقة ![]() “تغير علامتها”، هذا يعني أيضًا تغيير في اتجاه ازدياد أو نقصان الدالة
“تغير علامتها”، هذا يعني أيضًا تغيير في اتجاه ازدياد أو نقصان الدالة ![]() , مثل في الحالة 1.:
, مثل في الحالة 1.:
المشتقة إلى اليسار من ![]() موجبة، وإلى اليمين سالبة. يعني هذا أن الدالة
موجبة، وإلى اليمين سالبة. يعني هذا أن الدالة ![]() تزداد إلى اليسار من
تزداد إلى اليسار من ![]() وتنقص إلى اليمين. لازم تكون الصورة شكلها كده:
وتنقص إلى اليمين. لازم تكون الصورة شكلها كده: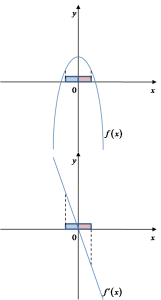 في الرسم البياني أعلاه عندنا رسم بياني للدالة
في الرسم البياني أعلاه عندنا رسم بياني للدالة ![]() (فوق) ومشتقتها
(فوق) ومشتقتها ![]() . ملاحظين أن في “الجوار الأيسر” لنقطة
. ملاحظين أن في “الجوار الأيسر” لنقطة ![]() (الموضح باللون الأزرق) المشتقة
(الموضح باللون الأزرق) المشتقة ![]() تأخذ قيم موجبة، والدالة
تأخذ قيم موجبة، والدالة ![]() في ازدياد. وفي “الجوار الأيمن” للنقطة
في ازدياد. وفي “الجوار الأيمن” للنقطة ![]() (الموضح باللون الأحمر) المشتقة
(الموضح باللون الأحمر) المشتقة ![]() تأخذ قيم سالبة، والدالة
تأخذ قيم سالبة، والدالة ![]() في تناقص.
في تناقص.
واضح أن هذا التغيير لازم يعني دائمًا وجود الحد الأقصى في نقطة ![]() .
.
النهاية
وأنا بكتب هذا المنشور استفدت من…
1. “حساب التفاضل والتكامل. المجلد الأول.” G.M. Fichtenholz. الطبعة 1966.
اضغط هنا لتذكر الشرط الضروري لوجود القيمة القصوى (المحاضرة السابقة) <–
اضغط هنا لرؤية شر ح كيفية استخدام المشتقات من الدرجات العليا لتحديد القيم القصوى >–
