نظام المعادلات بمعامل لتحديد

Krystian Karczyński

مؤسس ورئيس موقع eTrapez.

حاصل على درجة الماجستير في الرياضيات من الجامعة التقنية في بوزنان (بولندا). معلم خصوصي للرياضيات بخبرة عديدة سنوات. مبتكر أول دورات eTrapez، التي حققت شعبية كبيرة بين الطلاب في جميع أنحاء بولندا.

يعيش في شتشيتسين (بولندا). يحب النزهات في الغابة، الاستجمام على الشاطئ، وركوب الكاياك.

احسب المعامل ‘a’ في نظام المعادلات أعلاه مع العلم أنه متناقض.

بدلاً من الشروع بشكل منهجي في حساب رتبة المصفوفة الرئيسية، نحدد رتبة المصفوفة المكملة:

…إنها تساوي اثنين، لأنه يمكن استخراج محدد غير صفري من الدرجة الثانية من هذه المصفوفة (ولا يمكن الحصول على أكبر من ذلك):

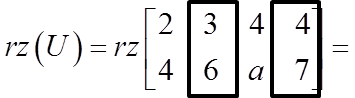
لذا فإن رتبة المصفوفة المكملة تساوي 2.

تطبيق نظرية كرونيكر-كابيلي

ما هي رتبة المصفوفة الرئيسية إذاً؟

نعلم أن النظام متناقض، ووفقًا لـ نظرية كرونيكر-كابيلي نعلم أنه سيكون متناقضًا عندما تكون رتبة المصفوفة الرئيسية مختلفة عن رتبة المصفوفة المكملة. ونعلم أيضًا أن رتبة المصفوفة الرئيسية دائمًا أقل أو تساوي رتبة المصفوفة المكملة (المصفوفة الرئيسية مضمّنة في المكملة). لذا يجب أن تكون رتبة المصفوفة الرئيسية 1 أو 0 (لتكون مختلفة عن رتبة المصفوفة المكملة).

ستكون رتبة المصفوفة الرئيسية:

نرى أنها بالتأكيد لن تكون 0 (فقط رتبة المصفوفة الصفرية تساوي 0) – لذا يجب أن تكون تساوي 1. ستكون الرتبة تساوي واحدًا عندما يكون الصف الأول والثاني متناسبين (سنحذف أحدهما حينها). نرى أن الصف الأول مضروب في اثنين يعطي الصف الثاني، إذا كان a يساوي 8 فقط.

لذا بسرعة ودون حسابات كبيرة نصل إلى الإجابة: