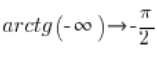الدوال الدائرية العكسية (محاضرة – فيديو)
الموضوع: الدوال الدائرية العكسية
ملخص
في هذه المحاضرة، سأقوم بتقديم مفهوم الدوال الدائرية العكسية: arcsinx, arccosx, arctgx, arcctgx. هذه الدوال هي معكوس الدوال المثلثية.
المحاضرة تتكون من جزئين. في الجزء الأول، أشرح كيفية حساب قيم الدوال الدائرية العكسية بسرعة، بدون التعمق كثيرًا في الموضوع (تم إرفاق فيديو لهذه الجزء، مقتطف من دورة التكاملات المعينة وغير المعينة وتطبيقات التكاملات).
في الجزء الثاني، أشرح الدوال الدائرية العكسية بشكل أكثر دقة، وأعرض رسوماتها البيانية وما إلى ذلك.
لفهم المحاضرة، ستحتاج إلى:
- الدوال المثلثية (المدرسة الثانوية)
الجزء الأول
الدوال الدائرية العكسية – النسخة “السريعة”
الدوال الدائرية العكسية ببساطة هي دوال معكوسة للدوال المثلثية. يعني arcsinx هي الدالة العكسية لـ sinx.
يعني إذا كنا نعرف، على سبيل المثال، أن 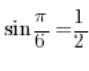 , فهذا يعني أن
, فهذا يعني أن ![]() .
.
وهكذا دواليك:
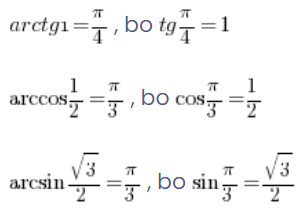
لذلك لدينا بعض خصائص الدوال الدائرية العكسية التي تسمح لنا بحساب قيمها حتى للأعداد السالبة:
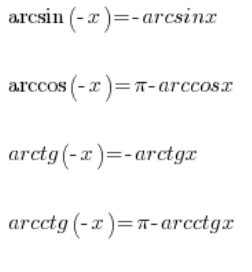
لذلك يمكننا أيضًا حساب:
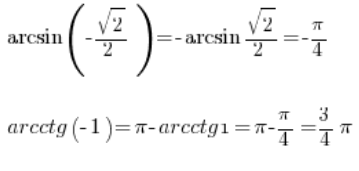
لذا، بوجود جدول الدوال المثلثية يمكننا بسهولة إيجاد قيم الدوال الدائرية العكسية بقراءته بالعكس.
أشرح هذا بالتفصيل في الفيديو هنا:
جدول القيم الأساسية للدوال المثلثية من الفيديو – قم بتنزيله هنا.
الجزء الثاني
الدوال الدائرية العكسية – النسخة الكاملة
مقدمة – لماذا الجزء الأول لا يكفي
يبدو أننا في الجزء الأول عرفنا كل دالة دائرية عكسية كمعكوسة للدالة المثلثية المقابلة لها.
دعونا نصوغ هذا بشكل أكثر رسمية. قلنا أن الدالة ![]() تأخذ القيمة
تأخذ القيمة ![]() , عندما تكون الدالة
, عندما تكون الدالة ![]() لهذه
لهذه ![]() تساوي
تساوي ![]() .
.
بالمثل:
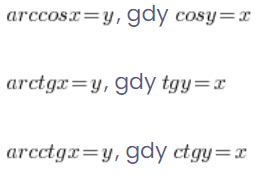
يعني إذا كنا نريد حساب ![]() نفكر في جيب التمام لأي زاوية يعطي
نفكر في جيب التمام لأي زاوية يعطي ![]() , ندرك أنه هو الزاوية
, ندرك أنه هو الزاوية ![]() ونحصل على النتيجة:
ونحصل على النتيجة: 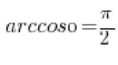 .
.
هل هذا يغطي جميع قيم الدوال الدائرية العكسية؟
بالطبع لا.
لنعد استعراض كل التفكير على أرقام محددة (ولننتقل ربما إلى arcsinx):
إذا كنا نريد حساب  نفكر في جيب أي زاوية يعطي
نفكر في جيب أي زاوية يعطي ![]() , ندرك أنه هو الزاوية
, ندرك أنه هو الزاوية ![]() ونحصل على النتيجة:
ونحصل على النتيجة:  .
.
أين المشكلة؟ في الجزء الغامق:
إذا كنا نريد حساب  نفكر في جيب أي زاوية يعطي
نفكر في جيب أي زاوية يعطي ![]() , ندرك أنه هو الزاوية
, ندرك أنه هو الزاوية ![]() ونحصل على النتيجة:
ونحصل على النتيجة:  .
.
للأسف، ليس فقط جيب الزاوية ![]() يساوي
يساوي ![]() .
.
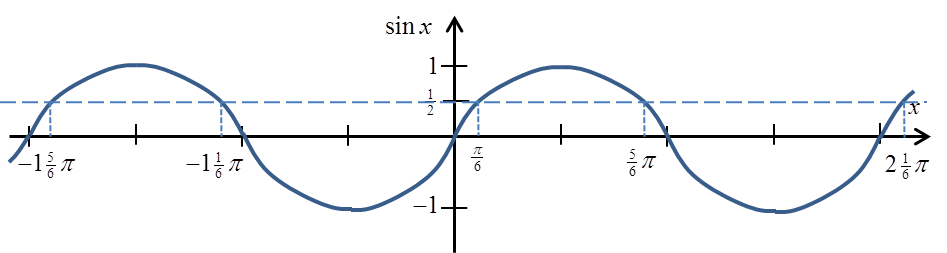
دعونا نذكر الرسم البياني للدالة sinx (لقد قمت بتحديد قيمة ![]() ):
):
يظهر لنا ومن المدرسة الثانوية أن جيب الزاوية يأخذ القيمة ![]() ليس فقط للزاوية
ليس فقط للزاوية ![]() ، ولكن أيضًا للزوايا:
، ولكن أيضًا للزوايا: 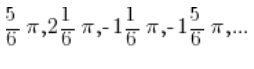
يعني 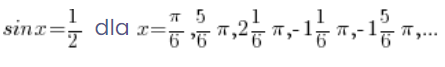
لنذكر مرة أخرى طريقتنا في حساب arcsin:
إذا كنا نريد حساب  نفكر في جيب أي زاوية يعطي
نفكر في جيب أي زاوية يعطي ![]() , ندرك أنه هو الزاوية
, ندرك أنه هو الزاوية ![]() ونحصل على النتيجة:
ونحصل على النتيجة:  .
.
لكننا الآن نعلم أن ليس فقط sin![]() يعطي
يعطي ![]() ، يبدو إذاً أن:
، يبدو إذاً أن:
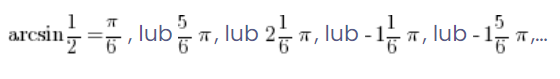
هذا يعني أن arcsinx ليس دالة على الإطلاق، لأنه لكل قيمة مدخلة يكون هناك عدة قيم ناتجة!
تقديم إجابة واضحة على السؤال “كم يساوي arcsin لشيء ما” سيكون مستحيلاً تماماً في هذه الحالة.
من السهل أيضاً تخيل أن مشكلة مشابهة تنطبق على كل دالة من الدوال المثلثية.
لو سمينا الأمر بمصطلحات أكثر احترافية: هذه الدوال ليست متباينة، لذا لا توجد دوال عكسية لها. في كل دالة مثلثية، كل قيمة يتم الوصول إليها لعدد لا نهائي من المدخلات (هي دورية، أليس كذلك؟)، لذا عند محاولة تحديد دوالها العكسية نحصل على عدد لا نهائي من القيم لكل مدخل. وهذا غير ممكن في الدوال.
ماذا نفعل؟
الأمر بسيط، لدرجة أنه يبدو بدائيًا. يمكننا قطع كل دالة مثلثية للحصول على دالة متباينة كنتيجة.
لذلك، دعونا نعرف بشكل صحيح جميع الدوال العكسية الأربع:
arcsinx
لنتذكر الرسم البياني لدالة sinx:
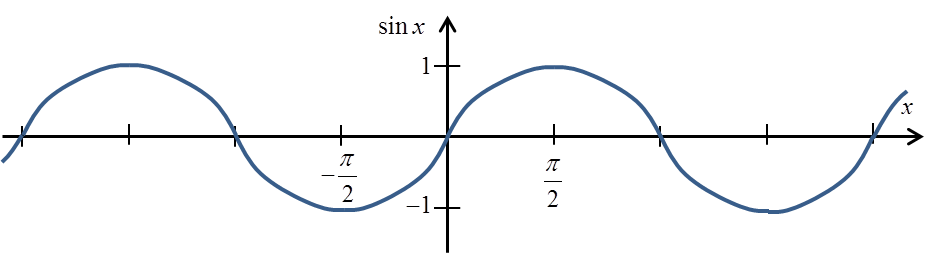
إذا اتفقنا على قطعها على سبيل المثال في الفترة ![]() ، نحصل على الرسم البياني التالي:
، نحصل على الرسم البياني التالي:
![Wykres sinx w przedziale [0,pi] Obraz3](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz33.png)
لسوء الحظ، هذا ليس ما نريده، لأنه ليس الرسم البياني لدالة متباينة، والمشكلة مع القيمة ![]() ما زالت قائمة:
ما زالت قائمة:
![Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2 Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz41.png)
لذا نتفق على قطع دالة sinx بشكل مختلف، إلى المدخلات 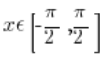 :
:
![Wykres funkcji sinx dla x należących do [-pi/2,pi/2] Wykres funkcji sinx dla x należących do [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz51.png)
الآن أصبحت دالة متباينة ولها دالة عكسية arcsinx.
يبدو الرسم البياني لدالة arcsinx تقريبًا هكذا:

مجالها هو الفترة ![]() غير موجود.
غير موجود.
التعريف الدقيق لدالة arcsinx هو إذن:
![]() .
.
arccosx
دالة cosx أيضًا ليست دالة متباينة:
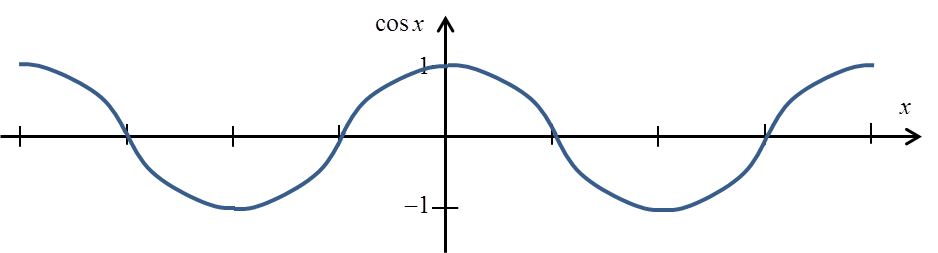
للحصول على دالة متباينة يجب علينا قطعها إلى الفترة ![]() :
:
![Wykres funkcji cosx obciętej do przedziału [0,pi] Wykres funkcji cosx obciętej do przedziału [0,pi]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz8.png)
بهذا الشكل، تكون الدالة متباينة ولها دالة عكسية arccosx.
الرسم البياني لها سيكون تقريبًا:
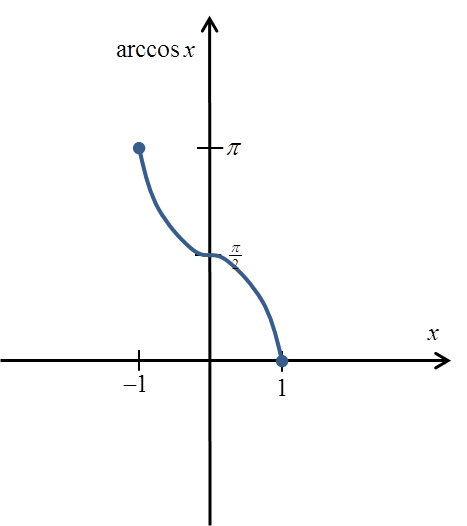
وتعريفها الدقيق:
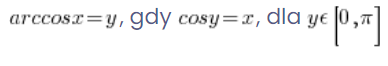 .
.
arctgx
يبدو الرسم البياني لدالة tgx هكذا:

أيضًا ليست دالة متباينة! يمكننا قطعها بالطريقة التالية:
![Wykres funkcji tgx obięty do przedziału [-pi/2,pi/2] Wykres funkcji tgx obięty do przedziału [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz111.png)
بهذا الشكل نحصل على دالة متباينة.
الرسم البياني لدالة arctgx يبدو هكذا:

وتعريفها الدقيق هو:
![]() ، لـ y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right).
، لـ y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right).
نلاحظ أيضًا أنه من الرسم البياني تنشأ بعض الخصائص المثيرة للاهتمام، مثل:
- مجال دالة arctgx هو مجموعة الأعداد الحقيقية (يمكن حساب arctg من أي عدد)


arcctgx
من الرسم البياني لدالة ctgx:

نقطع الجزء المتباين:
الرسم البياني لدالة arcctgx يبدو هكذا:
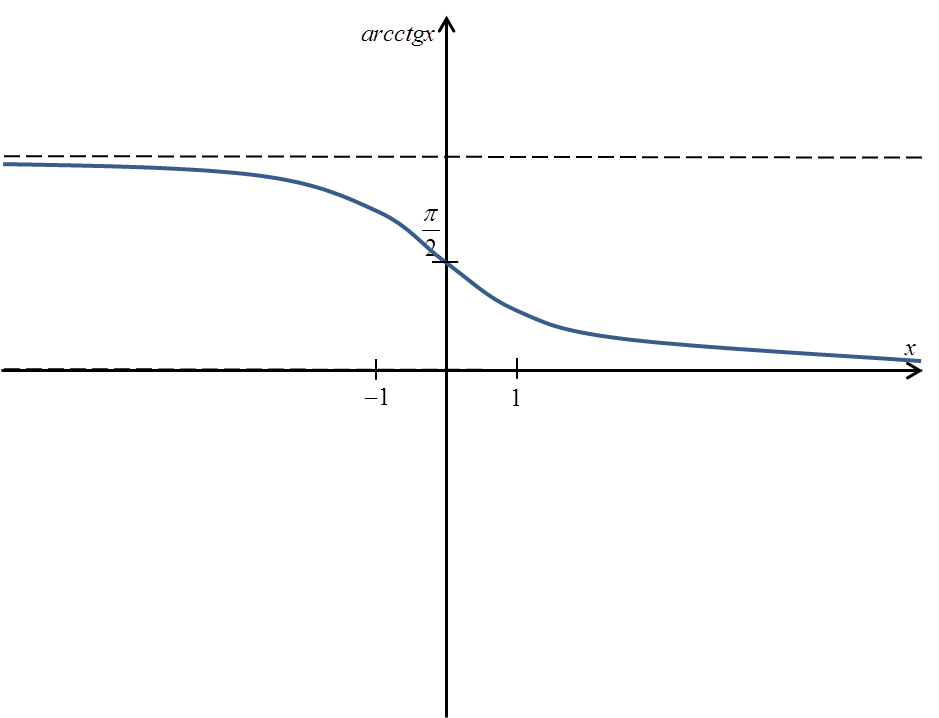
تعريف arcctgx الدقيق سيكون:
![]() .
.
نرى أن:
- مجال دالة arcctgx هو مجموعة الأعداد الحقيقية (يمكن حساب arcctg من أي عدد)


ملحوظة
في العديد من الآلات الحاسبة وفي العروض الرياضية بشكل عام (خاصة الغربية)، لا يتم تمييز الدوال العكسية للدوال المثلثية بكلمة “arcus”، بل بالأس -1. على سبيل المثال، يتم كتابة arcsinx كـ ![]() . إذا كنت تعلم ما يدور حوله الأمر، فلا مشكلة. ولكن يمكن أن ترتكب خطأ كبيراً وتخلط بين الدالة العكسية لـ sinx والدالة
. إذا كنت تعلم ما يدور حوله الأمر، فلا مشكلة. ولكن يمكن أن ترتكب خطأ كبيراً وتخلط بين الدالة العكسية لـ sinx والدالة ![]() – وهي دالة مختلفة تمامًا عن arcsinx.
– وهي دالة مختلفة تمامًا عن arcsinx.