Rząd macierzy Wykład 4
Temat: Układy równań liniowych z parametrem
Streszczenie
W artykule pokażę, jak w układach równań liniowych z parametrem określać ich liczbę rozwiązań przy pomocy rzędów macierzy (a nie jak na ogół wzorami Cramera).
Układy równań liniowych z parametrem
Układa równań liniowych z parametrem, na przykład:
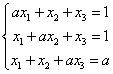 można rozpoznać po uroczej literce
można rozpoznać po uroczej literce ![]() , albo:
, albo: ![]() . Dla różnych wartości a (np.
. Dla różnych wartości a (np. ![]() ) otrzymamy różne rozwiązania układu. Być może dla niektórych wartości
) otrzymamy różne rozwiązania układu. Być może dla niektórych wartości ![]() otrzymamy układ sprzeczny, który nie ma rozwiązań. Być może dla niektórych wartości
otrzymamy układ sprzeczny, który nie ma rozwiązań. Być może dla niektórych wartości ![]() otrzymamy układ nieoznaczony, czyli taki, który ma nieskończenie wiele rozwiązań.
otrzymamy układ nieoznaczony, czyli taki, który ma nieskończenie wiele rozwiązań.
Nasze zadanie polega na ogół nie na rozwiązywaniu układu, tylko na określeniu, dla jakich wartości parametru układ ma 1 rozwiązanie (jest oznaczony), nieskończenie wiele rozwiązań (jest nieoznaczony), a dla jakich nie ma rozwiązań (jest sprzeczny).
Liczba rozwiązań układu zależna od rzędu macierzy
Do wyznaczenie liczby rozwiązań układu możemy wykorzystać wzory Cramera i wyznaczników, ale w niektórych układach wygodniejsze będzie skorzystanie z twierdzenia Kroneckera-Capellego. Przypomnijmy, że z tego twierdzenia wynika, że…
1. Układ jest oznaczony (ma 1 rozwiązanie), gdy:
![]() – rząd macierzy głównej jest równy rzędowi macierzy uzupełnionej i jest równy liczbie niewiadomych
– rząd macierzy głównej jest równy rzędowi macierzy uzupełnionej i jest równy liczbie niewiadomych
2. Układ jest nieoznaczony (ma nieskończenie wiele rozwiązań), gdy:
![]() – rząd macierzy głównej jest równy rzędowi macierzy uzupełnionej i jest mniejszy od liczby niewiadomych
– rząd macierzy głównej jest równy rzędowi macierzy uzupełnionej i jest mniejszy od liczby niewiadomych
3. Układ jest sprzeczny (brak rozwiązań), gdy:
![]() – rząd macierzy głównej jest różny od rzędu macierzy uzupełnionej
– rząd macierzy głównej jest różny od rzędu macierzy uzupełnionej ![]()
Ogólna metoda postępowania
Aby wykorzystać rząd macierzy do określenia liczby rozwiązań równania w zależności od parametru, będziemy postępowali następująco:
– wyznaczali rząd macierzy głównej rz(A)
– określali, dla jakich wartości parametru rząd macierzy głównej rz(A) przyjmuje różne wartości
– wyznaczali rząd macierzy uzupełnionej
– określali, dla jakich wartości parametru rząd macierzy uzupełnionej rz(U) przyjmuje różne wartości
– określali liczby rozwiązań układu równań w zależności od parametru korzystając z wniosków z twierdzenia Kroneckera-Capellego
Przed pójściem dalej przypomnij sobie koniecznie, jak obliczało się rząd macierzy!
Przykład
Określmy liczbę rozwiązań w zależności od parametru a w układzie:
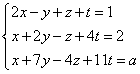 Na początku obliczamy rząd macierzy głównej A, czyli:
Na początku obliczamy rząd macierzy głównej A, czyli:
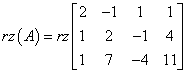
Rząd tej macierzy wyjdzie (po obliczeniu) równy 2. Zauważmy, że rząd macierzy głównej nie zależy w ogóle od parametru a. Przyjmuje po prostu zawsze wartość 2. Nie rozpisujemy więc, że dla pewnych a jest równy 1, dla innych 2, a dla innych 3. On jest po prostu zawsze równy 2 dla dowolnego a. Można zapisać:
![]()
Teraz liczymy rząd macierzy uzupełnionej U, czyli:
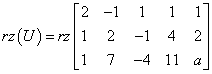
Będzie to już trochę trudniejsze, bo w macierzy, której rząd mamy policzyć występuje parametr a. Nie przejmujemy się jednak tym – traktujemy a jak zwykłą liczbę. „Wyzerujmy” na przykład trzecią kolumnę (pierwszy wiersz dodajemy do drugiego i pierwszy wiersz mnożymy przez 4 i dodajemy do trzeciego). Otrzymamy:
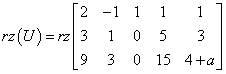
Zauważmy, że w ostatniej kolumnie działamy najnormalniej w świecie: 1 mnożymy przez 4 i dodajemy do a. Teraz wykreślamy pierwszy wiersz i trzecią kolumnę (zgodnie z zasadami obliczania rzędów) i zwiększamy rząd macierzy o 1. Mamy:
![]()
Teraz „zerujemy” drugą kolumnę, mnożąc pierwszy wiersz przez -3 i dodając do drugiego.
![]()
Po wykreśleniu trzeciej kolumny otrzymamy:
![]() Teraz zwróćmy uwagę, że rząd macierzy, jaka nam pozostała po tych wszystkich wykreśleniach zależy od parametru a.
Teraz zwróćmy uwagę, że rząd macierzy, jaka nam pozostała po tych wszystkich wykreśleniach zależy od parametru a.
Jeżeli a będzie równe 5, macierz będzie składała z samych zer, a rząd macierzy będzie wtedy równy 0. W tym przypadku rząd macierzy uzupełnionej będzie równy 2.
Jeżeli a będzie jednak różne od 5, macierz będzie miała element niezerowy, a rząd macierzy będzie wtedy równy 1.W tym przypadku rząd macierzy uzupełnionej będzie równy 3.
Można to zapisać:
![]() dla
dla ![]()
![]() dla
dla ![]() różnego od
różnego od ![]()
Podsumowując wartości rzędów macierzy głównej i uzupełnionej otrzymujemy:
![]() dla
dla ![]()
![]() i
i ![]() dla
dla ![]() różnego od
różnego od ![]()
Czyli układ ma nieskończenie wiele rozwiązań dla ![]() (bo wtedy rzędy macierzy są równe i mniejsze od liczby niewiadomych), a nie ma w ogóle rozwiązań dla
(bo wtedy rzędy macierzy są równe i mniejsze od liczby niewiadomych), a nie ma w ogóle rozwiązań dla ![]() różnego od
różnego od ![]() (bo wtedy rządy macierzy są różne).
(bo wtedy rządy macierzy są różne).
Przypadek, gdzie układ ma 1 rozwiązanie nie zachodzi nigdy.

PiotrLenarczyk
Jak byłem na inżynierskich to wykładał starszy, łysawy doktor – mówiło się, że jak on Cię nie nauczy matematyki, to lepiej dać sobie spokój ze studiowaniem. E-trapez spoko, ale na co to komukolwiek ( poza egzaminem ), jak nic z tego praktycznego nie wynika? Zastosowanie by się przydało.Post Scriptum: programowanie, czy tam bardziej współczesne podejście do zagadnienia ( typu: BLAS, cuSolver, et cetera ), to jednak temat jedynie dla specjalistów.
HBR
Rząd macierzy A wynosi 3 a nie 2
HBR
a nie, jednak jest dobrze 🙂
t3t
mi tez wyszło 3 o co chodzi?
Rafał
A co jeśli mamy parametr także w macierzy głównej?
x+ay-3z=0
x+y+z=0
3x+ay-z=0
Karolina
A co jeśli muszę rozwiązać układ równań, identyczny jak Pana, tylko w drugim równaniu wynik to a, natomiast w trzecim wynik to a^2?
Jacek
Swietne wytlumaczenie krok po kroku. Zastanawiam sie jak bedziemy jechac dalej jesli chcemy znalezc teraz rozwiazanie tego ukladu ktore bedzie zawieralo te dwa parametry. Zakladam, ze wracamy do macierzy glownej A i wybieramy z niej dowolny minor stopnia 2 o niezerowym wyznaczniku i budujemy uklad rownan? wtedy dostajemy tylko dwa uklady rownan w kazdym po dwa parametry. Czy tak?
Daniel
Nie wiem czy dobrze, ale parametr „a” wynosi 2. Jak wstawisz za „a” 2 to wtedy jest nieskończenie wiele rozwiązań bo R(A) i R(U) wynosi 3. Rzędy są wiec niższe od liczby niewiadomych.
Jak „a” jest różne od dwóch to R(A) i R(U) wynosi 4 i masz jedno rozwiązanie. A czy zachodzi sytuacja że układ jest sprzeczny to nie wiem…..
Oczywiście to co napisałem to tylko moja sugestia….
Pozdrawiam
Romek
Treść zadania brzmi: Określ liczbę rozwiązań, w zależności od a.
6x + 5y + z – 2w = 1
x + 2y + z + 6w = 2
-x – 4y + 3z + 4w = -1
ax + 6y – 2z + 2w = 3
Policzyłem rząd macierzy głównej i wyszedł mi 4 – jednak po skreśleniu kolumny zawierającej a
Policzyłem rząd macierzy uzupełnionej i wyszedł mi 3 – tym razem po wykreśleniu wiersza zawierającego a
Proszę (wiem, że o wiele) o rozwiązanie takiego przykładu bądź o wskazówki. Jak zinterpretować powyższe.
Czy słusznie postąpiłem? – Co oznacza wykreślenie parametru w obliczaniu rzędów w takim zadaniu?