W tym poście będę kontynuował tematykę zagadnień ze szkoły średniej, na które – być może – nie miałeś położonego zbyt wielkiego nacisku, a które bardzo ułatwią Ci życie na studia.
To już część 5 – jeśli wskoczyłeś tutaj dopiero teraz możesz zerknąć na 4 poprzednie posty 🙂
Tutaj zajmę się obustronnym mnożeniem i dzieleniem nierówności.
Dzielenie nierówności? A to już chyba wiem, o co chodzi…
No tak. Wszyscy już wiemy (chociaż czasami zapominamy) o zmianie znaku nierówności przy mnożeniu/dzieleniu jej przez liczbę ujemną.
Na przykład:
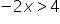 /:(-2)
/:(-2)
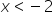 (zmienił się znak nierówności, bo podzieliłem obie strony przez liczbę ujemną)
(zmienił się znak nierówności, bo podzieliłem obie strony przez liczbę ujemną)
albo:
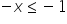 /
/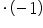
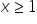 (znak nierówności się zmienił po pomnożeniu obu stron przez liczbę ujemną)
(znak nierówności się zmienił po pomnożeniu obu stron przez liczbę ujemną)
Co jednak z mnożeniem i dzieleniem nie przez LICZBĘ, tylko przez ZMIENNĄ, na przykład:
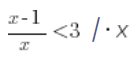
Możemy zrobić takie mnożenie i wyjść na:
![]()
…?
Prawidłowa odpowiedź to: NIE, NIE MOŻEMY.
Pamiętamy zasadę: „Jeśli mnożymy przez dodatnią nie zmieniamy znaku, jeśli mnożymy przez ujemną zmieniamy”. Mnożąc przez zmienną ![]() NIE WIEMY, czy mnożymy przez liczbę dodatnią, czy ujemną. Zmienna
NIE WIEMY, czy mnożymy przez liczbę dodatnią, czy ujemną. Zmienna ![]() może być równa -100, a może być równa także 15. To, że nie ma przed nią znaku minus niczego nie zmienia (może być i tak ujemna).
może być równa -100, a może być równa także 15. To, że nie ma przed nią znaku minus niczego nie zmienia (może być i tak ujemna).
Jeśli tego nie wiemy, nie możemy przechodzić na…
![]()
…bo na taką nierówność moglibyśmy wyjść tylko wtedy, kiedy mnożylibyśmy przez liczbę dodatnią (nie zmieniając znaku), a tego NIE WIEMY.
Analogiczna zasada obowiązuje w dzieleniu, nie możemy więc wykonać sobie czegoś takiego:
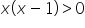 /:x
/:x
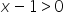
…bo, jeszcze raz powtórzmy: nie wiemy, czy x jest liczbą dodatnią, czy ujemną.
Podsumowując więc
Nie dzielimy obustronnie nierówności przez zmienne.
I jeszcze….
Ciekawostka
Jeżeli – skądinąd – mielibyśmy informację, że zmienna (albo całe wyrażenie) przez które obustronnie chcemy pomnożyć/podzielić JEST zawsze dodatnie (albo ujemne) możemy sobie śmiało mnożyć/dzielić.
Na przykład jeśli dziedziną (o dziedzinie będzie jeszcze post powtórkowy później) ![]() jest zbiór liczb
jest zbiór liczb ![]() , to wiemy, że
, to wiemy, że ![]() jest na pewno dodatni.
jest na pewno dodatni.
Wtedy MOŻEMY machnąć sobie…
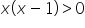 /:x
/:x
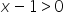
…pamiętając jednak o tym, żeby w otrzymanym zbiorze rozwiązań uwzględnić dziedzinę (wziąć z niego tylko ![]() .
.



8 Komentarzy
Krystian Karczyński
@Bob Tak, oczywiście, poprawiłem i dziękuję za zwrócenie uwagi.
Bob
W tym miejscu jest błąd
albo:
zakładam że miał Pan na myśli –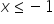 na samym początku prawda ?
na samym początku prawda ?
Artur
Na Pańskim kursie Liczb Zespolonych spotkałem się z obustronnym dzieleniem przez jednostkę urojoną „i”.
I tak zastanawiam się jak to jest z tym dzieleniem. Skoro i^2 to -1, a i = \sqrt(-1), to do końca nie wiadomo czy dzieląc przez „i” dzielimy przez liczbę ujemną, bo przecież pierwiastek z takowej w rzeczywistych nie istnieje ;).
No, ale jakbyśmy to sobie wszystko do kwadratu podnieśli (obie strony nierówności) i podzielili przez i^2 które przecież wynosi -1, to znak wypadałoby zmienić, prawda?
Z góry dziękuję za odpowiedź, kurs fajny 🙂
Krystian Karczyński
Cześć!
Dzięki za pytanie. Serio jest gdzieś tam dzielenie przez „i”? Może jest ale na pewno w RÓWNOŚCI, a nie w NIERÓWNOŚCI.
Mnożyć i dzielić równości przez liczby dodatnie, ujemne i takie, o których nie wiem, czy są dodatnie, czy ujemne można bez problemu (no chyba, że nie chcemy po takim pomnożeniu „zepsuć” wykresu funkcji po lewej stronie równania – jak pokazuję w moim Kursie Pochodnych).
Problem jest tylko z dzieleniem i mnożeniem nierówności, w których nie możemy np. podzielić przez 'x’, gdy nie wiemy, czy x jest liczbą dodatnią, czy ujemną.
Z zespolonymi liczbami w ogóle nie bawimy się w nierówności – bo nie określamy liczb zespolonych nie-rzeczywistych jako „dodatnich”, albo „ujemnych”, albo „większych” albo „mniejszych” 🙂
Artur
O proszę.
Krystian Karczyński
Ma Pan całkowitą rację, ten ostatnie przykład z Lekcji 7 absolutnie nie powinien znaleźć się w Kursie, bo wyszła z niego nierówność zespolona…
Czyli cały przykład jest źle ułożony przeze mnie i nie da się go „rozwiązać”.
Wszystkie wcześniejsze nierówności są O.K., bo rachują na sprzężeniach, częściach rzeczywistych i urojonych – czyli liczbach rzeczywistych.
Przepraszam i bardzo dziękuję za świetne i trafne pytanie.
Krystian Karczyński
Tak, tak, zgadza się o to mi chodziło. Rozwiązanie nierówności x-1>0 to zbiór \left(1,+{\infty}\right), dziedzina to zbiór \left(0,+{\infty}\right), czyli rozwiązanie CAŁEJ nierówności to:
\left(1,+{\infty}\right) (część rozwiązania ostatniej nierówności i dziedziny)
Mateusz
…pamiętając jednak o tym, żeby w otrzymanym zbiorze rozwiązań uwzględnić dziedzinę:
Mamy dwa warunki:
x>1 i x należy (0, nieskończoność) więc rozwiązaniem będzie zbiór x należy (1, nieskończoność)
To tak a propos ostatnich dwóch linijek…