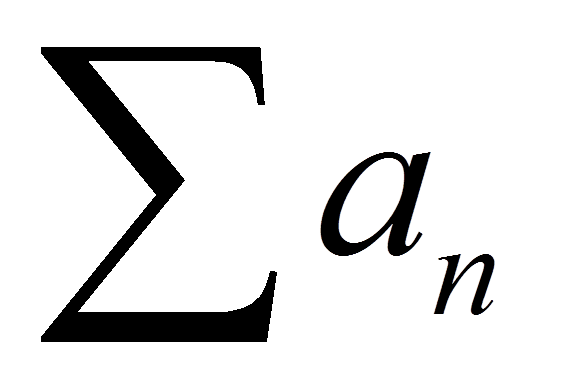
5 Kryteriów Zbieżności Szeregów
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
 Jest sobie szereg \sum{{{a}_{n}}} o wyrazach nieujemnych. Mamy sprawdzić, czy jest on zbieżny. Mamy do dyspozycji albo definicję (katorga), albo kryteria (spacer po łące).
Jest sobie szereg \sum{{{a}_{n}}} o wyrazach nieujemnych. Mamy sprawdzić, czy jest on zbieżny. Mamy do dyspozycji albo definicję (katorga), albo kryteria (spacer po łące).
Skupmy się na kryteriach.
W moim Kursie Szeregów pokazałem najczęściej używane:
Oczywiście nie oznacza to, że lista możliwych kryteriów zbieżności została w ten sposób wyczerpana. W tym poście zajmę się pozostałymi, wprowadzanymi w podręcznikach i przez niektórych profesorów.
Są takie przykłady, w których TYLKO zastosowanie jakiegoś wymyślnego kryterium pozwoli Ci określić zbieżność. Są profesorzy na studiach, którzy dają na egzaminach takie przykłady.
Przerobię:
- Kryterium “ilorazowe” (z nazewnictwem jest trochę różnie, o czym później)
- Kryterium “porównawcze ilorazowe”
- Kryterium Raabego
- Kryterium Bertranda
- Kryterium Jermakowa
Zaczynam:
1. Kryterium ilorazowe
Jeżeli mamy dwa szeregi \sum{{{a}_{n}}} i \sum{{{b}_{n}}} , oraz istnieje granica:
\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}}wtedy jeżeli:
- 0<\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}}<\infty oba szeregi są równocześnie albo zbieżne, albo rozbieżne
- \underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}}=0 ze zbieżności szeregu \sum{{{b}_{n}}} wynika zbieżność szeregu \sum{{{a}_{n}}}
- \underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}}=\infty z rozbieżności szeregu \sum{{{b}_{n}}} wynika rozbieżność szeregu \sum{{{a}_{n}}}
W praktyce robota z kryterium wygląda tak, że mam na wejściu jakiś szereg \sum{{{a}_{n}}} i muszę sam wykombinować taki szereg \sum{{{b}_{n}}} , o znanej już z góry zbieżności (lub rozbieżności), żeby granica \underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}} określiła mi zbieżność/rozbieżność szeregu \sum{{{a}_{n}}} .
Przykład 1
Zbadaj zbieżność szeregu \sum\limits_{n=1}^{\infty }{\left( \ln \left( n+1 \right)-\ln n \right)}
Wyraz \left( \ln \left( n+1 \right)-\ln n \right) podzielę przez \frac{1}{n} . O szeregu \sum\limits_{n=1}^{\infty }{\frac{1}{n}} wiem już, że jest to szereg rozbieżny (jest to szereg harmoniczny).
\underset{n\to \infty }{\mathop{\lim }}\,\frac{\ln \left( n+1 \right)-\ln n}{\frac{1}{n}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\ln \frac{n+1}{n}}{\frac{1}{n}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\ln \left( \tfrac{n}{n}+\tfrac{1}{n} \right)}{\frac{1}{n}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\ln \left( 1+\tfrac{1}{n} \right)}{\frac{1}{n}}A to już wprost ze wzoru \underset{x\to 0}{\mathop{\lim }}\,\frac{\ln \left( 1+x \right)}{x}=1 :
\underset{n\to \infty }{\mathop{\lim }}\,\frac{\ln \left( 1+\tfrac{1}{n} \right)}{\frac{1}{n}}=1Moja granica \underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}} z kryterium ilorazowego wyszła równa 1. Zgodnie z kryterium ilorazowym zatem szereg \sum\limits_{n=1}^{\infty }{\left( \ln \left( n+1 \right)-\ln n \right)} jest szeregiem rozbieżnym, ponieważ:
- \sum\limits_{n=1}^{\infty }{\frac{1}{n}} jest rozbieżny
- Granica \underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}}=1 , czyli oba szeregi są albo równocześnie zbieżne, albo równocześnie rozbieżne
- Czyli muszą być oba równocześnie rozbieżne
Przykład 2
Zbadaj zbieżność szeregu \sum\limits_{n=1}^{\infty }{\frac{1}{{{n}^{2}}-n}} .
Wyraz \frac{1}{{{n}^{2}}-n} podzielę przez \frac{1}{{{n}^{2}}} . O szeregu \sum\limits_{n=1}^{\infty }{\frac{1}{{{n}^{2}}}} wiem już z góry, że jest to szereg zbieżny (szereg Dirichleta – tłumaczę to w swoim Kursie ).
Mam:
\underset{n\to \infty }{\mathop{\lim }}\,\frac{\frac{1}{{{n}^{2}}-n}}{\frac{1}{{{n}^{2}}}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{1}{{{n}^{2}}-n}\frac{{{n}^{2}}}{1}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{n}^{2}}}{{{n}^{2}}-n}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{n}^{2}}}{{{n}^{2}}\left( 1-\tfrac{1}{n} \right)}=1Zatem na mocy kryterium porównawczego szereg \sum\limits_{n=1}^{\infty }{\frac{1}{{{n}^{2}}-n}} jest zbieżny.
Jest tak, dlatego, że:
- \sum\limits_{n=1}^{\infty }{\frac{1}{{{n}^{2}}}} jest zbieżny
- Granica \underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}}=1 , czyli oba szeregi są albo równocześnie zbieżne, albo równocześnie rozbieżne
- Czyli muszą być oba równocześnie zbieżne
2. Kryterium “porównawcze ilorazowe”
Tak je nazwałem, chociaż często przez “porównawcze ilorazowe” rozumie się te kryterium oczko wyżej, czyli moje “ilorazowe”. Nie o nazwy jednak chodzi, tylko o to, że:
Mamy dwa szeregi \sum{{{a}_{n}}} i \sum{{{b}_{n}}} . Jeżeli od pewnego n jest spełniona nierówność:
\frac{{{a}_{n+1}}}{{{a}_{n}}}\le \frac{{{b}_{n+1}}}{{{b}_{n}}}wtedy:
- ze zbieżności szeregu \sum{{{b}_{n}}} wynika zbieżność szeregu \sum{{{a}_{n}}}
- z rozbieżności szeregu \sum{{{a}_{n}}} wynika rozbieżność szeregu \sum{{{b}_{n}}}
3. Kryterium Raabego
Jest to mocne kryterium, a przynajmniej silniejsze od kryterium d’Alemberta. Oznacza to, że w niektórych przypadkach, gdy kryterium d’Alemberta nie roztrzyga o zbieżności szeregu, kryterium Raabego może to roztrzygnąć.
Mamy szereg \sum{{{a}_{n}}} . Liczymy granicę:
\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)Jeżeli:
- \underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)>1 wtedy szereg jest zbieżny
- \underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)<1 wtedy szereg jest rozbieżny
- \underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)=1 wtedy nie możemy roztrzygnąć zbieżności szeregu
Przykład 3
Zbadaj zbieżność szeregu \sum\limits_{n=1}^{\infty }{\frac{\left( 2n-1 \right)!!}{\left( 2n \right)!!}\frac{1}{2n+1}}
Ten dziwny znaczek: \left( 2n \right)!! oznacza taką specjalną silnię, w której mnożymy przez wyrazy o 2 mniejsze (a nie o jeden), na przykład: 10!!=10\cdot 8\cdot 6\cdot 4\cdot 2 .
Licząc ten szereg kryterium d’Alemberta otrzymał bym:
\underset{n\to \infty }{\mathop{\lim }}\,\frac{\frac{\left( 2n+1 \right)!!}{\left( 2n+2 \right)!!}\frac{1}{2n+3}}{\frac{\left( 2n-1 \right)!!}{\left( 2n \right)!!}\frac{1}{2n+1}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\left( 2n+1 \right)\left( 2n-1 \right)\left( 2n-3 \right)\cdot \ldots \cdot 1}{\left( 2n+2 \right)\left( 2n \right)\left( 2n-2 \right)\cdot \ldots \cdot 2}\frac{1}{2n+3}\frac{\left( 2n \right)\left( 2n-2 \right)\cdot \ldots \cdot 2}{\left( 2n-1 \right)\left( 2n-3 \right)\cdot \ldots \cdot 1}\frac{2n+1}{1}= =\underset{n\to \infty }{\mathop{\lim }}\,\frac{2n+1}{2n+2}\frac{2n+1}{2n+3}=1Czyli kryterium d’Alemberta jest tu bezradne.
Liczę granicę z kryterium Raabego:
\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{\frac{\left( 2n-1 \right)!!}{\left( 2n \right)!!}\frac{1}{2n+1}}{\frac{\left( 2n+1 \right)!!}{\left( 2n+2 \right)!!}\frac{1}{2n+3}}-1 \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{\left( 2n-1 \right)\left( 2n-3 \right)\cdot \ldots \cdot 1}{\left( 2n \right)\left( 2n-2 \right)\cdot \ldots \cdot 2}\frac{1}{2n+1}\frac{\left( 2n+2 \right)\left( 2n \right)\left( 2n-2 \right)\cdot \ldots \cdot 2}{\left( 2n+1 \right)\left( 2n-1 \right)\left( 2n-3 \right)\cdot \ldots \cdot 1}\frac{2n+3}{1}-1 \right)= =\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{\left( 2n+2 \right)\left( 2n+3 \right)}{{{\left( 2n+1 \right)}^{2}}}-1 \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{4{{n}^{2}}+10n+6}{{{\left( 2n+1 \right)}^{2}}}-\frac{{{\left( 2n+1 \right)}^{2}}}{{{\left( 2n+1 \right)}^{2}}} \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{4{{n}^{2}}+10n+6-\left( 4{{n}^{2}}+4n+1 \right)}{{{\left( 2n+1 \right)}^{2}}} \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{6n+5}{{{\left( 2n+1 \right)}^{2}}} \right)= =\underset{n\to \infty }{\mathop{\lim }}\,\frac{6{{n}^{2}}+5n}{{{\left( 2n+1 \right)}^{2}}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{n}^{2}}\left( 6+\tfrac{5}{n} \right)}{{{n}^{2}}{{\left( 2+\tfrac{1}{n} \right)}^{2}}}=\frac{6}{4}=\frac{3}{2}Zatem na mocy kryterium Raabego szereg \sum\limits_{n=1}^{\infty }{\frac{\left( 2n-1 \right)!!}{\left( 2n \right)!!}\frac{1}{2n+1}} jest zbieżny, bo granica \underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)>1 .
Przykład 4
Zbadaj zbieżność szeregu \sum\limits_{n=1}^{\infty }{\frac{n!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)}}
D’Alembert znowu jest tutaj żałośnie bezradny:
\underset{n\to \infty }{\mathop{\lim }}\,\frac{\frac{\left( n+1 \right)!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)\left( n+1\tfrac{1}{2} \right)}}{\frac{n!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\left( n+1 \right)n!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)\left( n+1\tfrac{1}{2} \right)}\frac{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)}{n!}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{n+1}{n+1\tfrac{1}{2}}=1A kryterium Raabego daje radę:
\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{\frac{n!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)}}{\frac{\left( n+1 \right)!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)\left( n+1\tfrac{1}{2} \right)}}-1 \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{n!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)}\frac{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)\left( n+1\tfrac{1}{2} \right)}{\left( n+1 \right)n!}-1 \right)= =\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{n+1\tfrac{1}{2}}{n+1}-1 \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{n+1\tfrac{1}{2}}{n+1}-\frac{n+1}{n+1} \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{\tfrac{1}{2}}{n+1} \right)=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\tfrac{1}{2}n}{n+1}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\tfrac{1}{2}n}{n\left( 1+\tfrac{1}{n} \right)}=\frac{1}{2}Czyli na mocy kryterium Raabego szereg \sum\limits_{n=1}^{\infty }{\frac{n!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)}} jest rozbieżny, bo granica \underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)<1 .
4. Kryterium Bertranda
Jest to kryterium jeszcze silniejsze od kryterium Raabego (zadziała w niektórych przypadkach, w których zawiedzie Raabe).
Mamy szereg \sum{{{a}_{n}}} . Liczymy granicę:
\underset{n\to \infty }{\mathop{\lim }}\,\ln n\left[ n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)-1 \right]Jeżeli:
- \underset{n\to \infty }{\mathop{\lim }}\,\ln n\left[ n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)-1 \right]>1 wtedy szereg jest zbieżny
- \underset{n\to \infty }{\mathop{\lim }}\,\ln n\left[ n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)-1 \right]<1 wtedy szereg jest rozbieżny
- \underset{n\to \infty }{\mathop{\lim }}\,\ln n\left[ n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)-1 \right]=1 wtedy nie możemy roztrzygnąć zbieżności szeregu
Jak widać, kryterium Bertranda jest silniejsze od Raabego, ale kosztem tego, że liczyć trzeba bardziej skomplikowaną granicę (tak samo jak Raabego było silniejsze od d’Alemberta kosztem skomplikowania granicy).
5. Kryterium Jermakowa
Kryterium wykorzystuje funkcje (podobnie) jak kryterium całkowe (omawiam je w moim Kursie). Nie potrzeba jednak do niego żadnych całek. Załóżmy, że mamy funkcję f\left( x \right) , utworzoną z ciągu {{a}_{n}} w szeregu \sum{{{a}_{n}}} ( {{a}_{n}}=f\left( n \right) ), nieujemną i malejącą – wszystko tak jak w kryterium całkowym. Wówczas…
Kryterium Jermakowa
Badamy funkcję:
\frac{f\left( {{e}^{x}} \right){{e}^{x}}}{f\left( x \right)}Jeżeli od pewnego x>{{x}_{0}}
- \frac{f\left( {{e}^{x}} \right){{e}^{x}}}{f\left( x \right)}\le q<1 wtedy szereg jest zbieżny (funkcja musi być ograniczona od góry ułamkiem właściwym)
- \frac{f\left( {{e}^{x}} \right){{e}^{x}}}{f\left( x \right)}\ge 1 wtedy szereg jest rozbieżny (funkcja musi być ograniczona od dołu liczbą 1)
Przykład 5
Zbadaj zbieżność szeregu \sum\limits_{n=2}^{\infty }{\frac{1}{n{{\ln }^{2}}n}}
Szereg można zrobić kryterium całkowym. Szybciej będzie jednak machnąć “Jermakowem”. Funkcja \frac{1}{x{{\ln }^{2}}x} spełnia założenia, bo ma wyrazy nieujemne dla x>2 i jest malejąc w tym przedziale.
Czyli tworzymy do niej funkcję z twierdzenia Jermakowa:
\frac{f\left( {{e}^{x}} \right){{e}^{x}}}{f\left( x \right)}=\frac{\tfrac{1}{{{e}^{x}}{{\ln }^{2}}{{e}^{x}}}{{e}^{x}}}{\tfrac{1}{x{{\ln }^{2}}x}}=\frac{\tfrac{1}{{{\left( \ln {{e}^{x}} \right)}^{2}}}}{\tfrac{1}{x{{\ln }^{2}}x}}=\frac{1}{{{\left( x\ln e \right)}^{2}}}\frac{x{{\ln }^{2}}x}{1}=\frac{1}{{{x}^{2}}}\frac{x{{\ln }^{2}}x}{1}=\frac{{{\ln }^{2}}x}{x}Wraz ze wzrostem x to wyrażenie dąży do 0 :
\underset{x\to \infty }{\mathop{\lim }}\,\frac{{{\ln }^{2}}x}{x}\underset{H}{\mathop{=}}\,\underset{x\to \infty }{\mathop{\lim }}\,\frac{{{\left( {{\ln }^{2}}x \right)}^{\prime }}}{{{\left( x \right)}^{\prime }}}=\underset{x\to \infty }{\mathop{\lim }}\,\frac{2\ln x\cdot \tfrac{1}{x}}{1}=\underset{x\to \infty }{\mathop{\lim }}\,\frac{2\ln x}{x}\underset{H}{\mathop{=}}\,\underset{x\to \infty }{\mathop{\lim }}\,\frac{{{\left( 2\ln x \right)}^{\prime }}}{{{\left( x \right)}^{\prime }}}=\underset{x\to \infty }{\mathop{\lim }}\,\frac{2}{x}=0Zatem z pewnością jest ograniczone od góry jakimś ułamkiem właściwym q , o którym mowa w twierdzeniu.
Zatem na mocy twierdzenia Jermakowa jest to szereg zbieżny.
Podsumowanie
Dodatkowych kryteriów zbieżności z tego postu nie traktuj jako kryteria alternatywne, do tych bardziej znanych, ale jak zawodników rezerwowych, którzy wchodzą do gry, kiedy podstawowy team zawodzi.
Są one przeważnie bardziej skomplikowane od swoich popularnych “zamienników” i wymagają użycia cięższej artylerii. Ale w matematyce i miłości wszystkie chwyty dozwolone 🙂
Bestsellery

Kurs Całki Oznaczone, Niewłaściwe i Zastosowania Całek
Studia / Autor: mgr Krystian Karczyński
39,00 zł
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.








Jaka jest różnica kiedy przy szeregu jest podane, że:albo zaczyna się od n=1, albo od n=2?
Badając zbieżność szeregu porównamy go z szeregiem ?Bardzo proszę o odpowiedz i objaśnienie.
porównamy go z szeregiem ?Bardzo proszę o odpowiedz i objaśnienie.
Mam pytanie, czym się różni warunek zbieżności algorytmu G-S od kryterium zbieżności algorytmu G-S ?
Jaka jest różnica między a
a  ? Bo jakoś nie potrafię rozgryźć poniższego:”Warunek konieczny zbieżności szeregu, ton-ty wyraz naszego szeregu toan = (- 1)n× 2, skąd , a więc “
? Bo jakoś nie potrafię rozgryźć poniższego:”Warunek konieczny zbieżności szeregu, ton-ty wyraz naszego szeregu toan = (- 1)n× 2, skąd , a więc “
Warunkiem koniecznym zbieżności szeregu jest
jest  .
.
Rozważany szereg jest szeregiem naprzemiennym
jest szeregiem naprzemiennym  , gdzie
, gdzie  . Do zbadania jego zbieżności stosujemy kryterium Leibnitza.
. Do zbadania jego zbieżności stosujemy kryterium Leibnitza.
Nie spotkałem się w teorii aby warunek konieczny był formułowany jako . W mojej ocenie nie jest to nawet potrzebne. Aby rzetelnie jednak odpowiedzieć na Pani pytanie musiałbym dokładnie wiedzieć o jakich szeregach mówimy. Być może wykładowca wprowadzając ten warunek uogólnił to na szeregi o wyrazach niedodatnich…
. W mojej ocenie nie jest to nawet potrzebne. Aby rzetelnie jednak odpowiedzieć na Pani pytanie musiałbym dokładnie wiedzieć o jakich szeregach mówimy. Być może wykładowca wprowadzając ten warunek uogólnił to na szeregi o wyrazach niedodatnich…
A ja mam pytanie innej kategorii przerabiałam Pański kurs na szeregi i wychodziły one dobrze ale ostanio miałam taki przykład na kolokwium, którego nie potrafiłam rozgryźć. Czy chciałby mi Pan pomóc go zrozumieć? Przykład wygląda tak ∑_(n=1)^∞▒〖(3^n-2^n)/(5^n-4^n )=〗
Zbieżność szeregu zbadamy korzystając z kryterium Cauchy’ego.
zbadamy korzystając z kryterium Cauchy’ego.
Obliczamy
Ponieważ więc na podstawie kryterium Cauchy’ego rozważany szereg jest zbieżny.
więc na podstawie kryterium Cauchy’ego rozważany szereg jest zbieżny.
witam, mam do Pana pytanie. właśnie przerabiam Pana kurs szeregów, zrobilam przyklady z pracy domowej oraz te przykłady które mialam zadane przez pana profesora. jezeli dajmy na to obliczam zbieznosc kryterium D’Alamberta i wyjdzie mi 1 to czy to oznacza ze wzielam złe kryterium? czy mogę po prostu zostawic taka odpowiedz? a może próbować rozwiązać jakimś innym sposobem?
W przykładzie 1. napisał Pan, że wprost ze wzoru… gdzie x dąży do 0, a w tym przykładzie n dąży do nieskończoności. Czy to nie robi różnicy?
W tym gotowym wzorze na granicę sam WYRAZ ma dążyć do zera. W przypadku tego przykładu jest ten warunek spełniony, bo przy lim dążącym do nieskończoności 1/n=0, więc wszystko się zgadza 🙂
Czy w przekładzie 5 nie jest konieczne sprawdzenie, czy aby x=1 nie jest asymptotą otrzymanej funkcji? Bo gdyby tak było to funkcja wcale nie musiałaby być ograniczona przez jakiś ułamek 🙂
Tak, oczywiście, w 100% ma Pan rację, bardzo celna uwaga, dzięki!
Oczywiście x=1 jest asymptotą prawostronną tej funkcji i oczywiście dlatego nie jest ona ograniczona w przedziale x>1 (wbrew temu, co niby “wykazałem”).
Problem leży już w doborze szeregu, jest: \sum\limits_{n=1}^{\infty }{\frac{1}{n{{ln }^{2}}n}}, a powinno być: \sum\limits_{n=2}^{\infty }{\frac{1}{n{{ln }^{2}}n}}(dwójka w dolnym indeksie znaku sumy). Przecież nie możemy “zacząć” od n=1, bo dostaniemy dzielenie przez zero.
Dalej przez tą jedynkę wziąłem sprawdzanie ograniczoności dla x>1, a trzeba było dla x>2 (a można było nawet dla x>100, zgodnie z kryterium).
Poprawiłem edytując post. Zwrócił Pan uwagę na ciekawy problem, który pominąłem – funkcja może nie być ograniczona w otoczeniu asymptoty pionowej i na to też oczywiście trzeba zwracać uwagę (chociaż wobec dowolności punktu x_0z kryterium nie ma to w praktyce aż tak dużego znaczenia). Jeszcze raz dziękuję.
heh panie Krystianie post fajny ale filmy jakoś lepiej się ogląda hehe nie trzeba czytać tak dużo haha. Jestem leniem a leniom czytać się nie chce a pana wiedza cenniejsza od złota