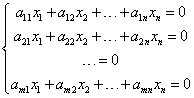
Układy równań jednorodne (liczba rozwiązań przy użyciu rzędu macierzy)
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Układy równań liniowych jednorodne to taki układy, w których wszystkie wyrazy wolne równe są 0. Wyglądają one tak:
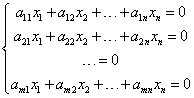
Na przykład:
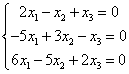
Możliwe liczby rozwiązań w układach równań liniowych
Przypomnijmy sobie, że w każdym układzie równań liniowych możliwe są trzy sytuacje:
1. Układ ma 1 rozwiązanie (kiedy rząd macierzy głównej = rząd macierzy uzupełnionej = liczba niewiadomych w układzie: ![]() )
)
2. Układ ma nieskończenie wiele rozwiązań (kiedy rząd macierzy głównej = rząd macierzy uzupełnionej i jest mniejszy od liczby niewiadomych w układzie ![]()
![]()
![]()
3.Układ nie ma rozwiązań (kiedy rząd macierzy głównej nie jest równy rzędowi macierzy uzupełnionej)
Macierz uzupełniona to macierz główna z dodaną kolumną wyrazów wolnych. W przypadku układu jednorodnego, będzie to kolumna z samymi zerami. Podczas liczenia rzędów można ją po prostu wykreślić i uzyskać w ten sposób samą macierz główną.
W naszym przykładzie rząd macierzy głównej równy jest:
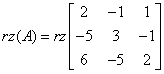
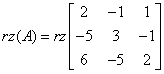
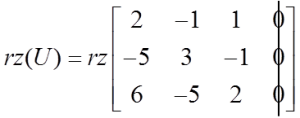
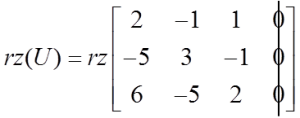
Na przykładzie widać, że ![]()
![]()
Możliwe liczby rozwiązań w układzie jednorodnym liniowym
Skoro tak, to w układzie równań jednorodnych zachodzić będą tylko sytuacje 1 lub 2. Układ zawsze będzie miał rozwiązania, pytanie tylko czy będzie to 1 rozwiązanie, czy nieskończenie wiele rozwiązań.
Idźmy dalej.
Zdefiniujmy sobie coś takiego, jak “rozwiązanie zerowe”. Rozwiązaniem zerowym nazwiemy takie rozwiązanie, w którym wartości wszystkich niewiadomych równe są 0.
Mówiąc o układach równań jednorodnych, zauważyć można, że:
Rozwiązanie zerowe jest zawsze rozwiązaniem układu jednorodnego.
Łatwo to sprawdzić: jeżeli za wszystkie niewiadome w równaniach wstawimy zera widać jasno, że każde równanie układu jednorodnego będzie spełnione, zawsze i w każdym układzie jednorodnym.
Jeżeli wiemy więc, że jednorodny układ równań liniowych ma 1 rozwiązanie (a jest tak, kiedy ![]()
![]()
![]()
Jeżeli zaś wiemy, że jednorodny układ równań liniowych ma nieskończenie wiele rozwiązań (a jest tak, kiedy ![]()
![]()
![]()
Jeżeli w zadaniu mamy więc polecenie: “sprawdź, czy układ jednorodny ma rozwiązania niezerowe”, wystarczy wykazać, że jest to układ nieoznaczony, w którym rząd macierzy głównej i uzupełnionej jest mniejszy od liczby niewiadomych.
W niektórych układach jest to bardzo proste, na przykład tutaj:
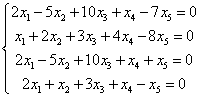
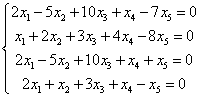
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.










Potrzbuje pomocy do dwoch zadan;
1.
czy punkty (1,2,2), (-1,1,1), (0,3/2, 1/2)
a) należą do płaszczyzny P:2×1-x2-x3+2=0.
b) P przechodzi przez początek układu współrzędnych.
2.
Dany jest jednorodny uklad równań Ax=0 o nieskończenie wielu rozwiązaniach
a) czy suma dwóch rozwiązań szczególnych tego układu też jest rozwiązaniem układu?
b) każde dwa rozwiązania szczególne są wektorami liniowo niezależnymi?
c) A może być macierze jednostkowa?
Na początek, polecam oczywiście mój Kurs Geometrii Analitycznej.
1.
Aby sprawdzić, czy punkt należy do płaszczyzny, wystarczy wstawić jego współrzędne do równania i sprawdzić, czy jest spełnione:
a)
Zaczynam od punktu

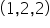

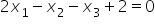
Równanie spełnione, zatem punkt

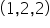
Dalej punkt
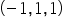
Zatem punkt nie należy do płaszczyzny.
Na końcu punkt
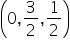
Zatem punkt należy do płaszczyzny.
b)
Zadanie sprowadza się do sprawdzenia, czy początek układu współrzędnych, tzn. punkt
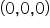
Czyli nie należy, czyli płaszczyzna nie przechodzi przez początek układu współrzędnych.
Chcialbym sie upewnic ze dobrze zrozumialem.
Czy to oznacza , ze jesli znamy jedynie rozwiazania macierzy to mozemy bez wyliczen ustalic czy macierz jest oznaczona czy nie?
Czy jesli zbior rozwiazan macierzy wynosi dla czterech niewiadomych (0,0,0,0) to uklad (jednorodny) jest zawsze oznaczony?
A gdy zbior ten wynosi np. (1, 7, 0, 9) to zawsze mamy do czynienia z ukladem nieoznaczonym?
Czy uklad jednorodny zawsze ma w tym zbiorze min 1 rozwiazanie ktore wynosi 0?
Witam, mam takie zadanie:
Aby jednorodne układ równań Anxn X=0 miał niezerowe rozwiązania macierz Anxn musi być ….
Cześć, mam taki problem w zadaniu.Treść: Zbadaj ilość rozwiązań i jeśli istnieją to je wskaż:
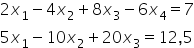
Mam problem z dwoma zadaniami w jedej z książek z matematyki
Udowodnij, że jeśli X1 i X2 są rozwiązaniami jednorodnego układu równań liniowych, to także wektor X1+X2 jest jego rozwiązaniem – nie wiem czy dobrze zrobiłem bo otrzymałem rozwiązanie zerowe.
Podaj przykład układu dwóch równań o 4 niewiadomych, który ma tylko jedno rozwiązanie bazowe – nie wiem od czego zacząć.
Witam,
Mając zadanie brzmiące: “W jakim przypadku układ równań jednorodny ma rozwiązanie niezerowe?”
Odpowiedź (po części zacytowana od Pana 🙂 ) będzie według Pana uznana za pełną?
“Układ ma rozwiązanie niezerowe gdy jest to układ nieoznaczony, w którym rząd macierzy głównej i uzupełnionej jest mniejszy od liczby niewiadomych”
Serdecznie pozdrawiam.
Tak.
Witam,
aby istniały rozwiązania niezerowe układu jednorodnego AX=0 i A(nxn)… nie rozumiem kompletnie nic, proszę o pomoc
Witam, bardzo proszę o odpowiedź.
A co jeśli mam układ 6 równań liniowych jednorodnych i 4 niewiadome? Ile rozwiązań może mieć ten układ i dlaczego?
Witam mam takie pytanie jak mam rozwiązać taki typ zadania.
Sprawdz (przy pomocy macierzy), czy podany układ równań liniowych jest sprzeczny.
przykład a) x + y =2
4x – y =5
3x – 7y =2
przykład b) x + y + 3z =2
4x – y -z =5
3x – 2y – 4z =3
Witam, sprawdzić, czy rzędy macierzy głównej i uzupełnionej dla tego układu są równe (jak nie są, to jest sprzeczny).
Co to są te macierze opisałem tutaj:
https://blog.etrapez.pl/macierze/rzad-macierzy-w-twierdzeniu-kroneckera-capellego/
Witam, prosiłbym o podpowiedź jak ugryźć zadanie typu:
1) Dla jakich wartości parametru podany układ jednorodny ma niezerowe rozwiązanie
2) Znajdź wszystkie wartości parametru, dla których podany układ niejednorodny ma tylko jedno rozwiązanie ( 1) i 2) są “rozmiarów” cramera)
i trudniejsze: 3) Znaleźć dodatnie rozwiązania układu równań:
x*(y^2)*(z^3)=2
(x^2)*(y^3)*(z^4)=4
(x^2)*y*z=2
Mam problem z zadaniem ” wyznacz zmienną y z układu równań:
x-4y-z=-3
2x-y+3z=4
4x+y+5z=6 ”
Czy mogę prosić o sposób rozwiązania tego zadania ?
Jasne, do układu:
\{ \begin{matrix}
& x-4y-z=-3 \\
& 2x-y+3z=4 \\
& 4x+y+5z=6 \end{matrix}
wystarczą zwykłe wzory Cramera.
Liczę wyznacznik główny (pokazuję, jak to się robi w moim Kursie, a liczę w WolframAlpha):
W=| \begin{matrix}
1 & -4 & -1 \\
2 & -1 & 3 \\
4 & 1 & 5 \end{matrix} |=-22
Ponieważ mam wyznaczyć tylko zmienną y, liczę tylko {{W}_{y}}:
{{W}_{y}}=| \begin{matrix}
1 & -3 & -1 \\
2 & 4 & 3 \\
4 & 6 & 5 \end{matrix} |=0
Czyli moje rozwiązanie to: y=\frac{{{W}_{y}}}{W}=\frac{0}{-22}=0, co potwierdza WolframAlpha.
Sory, ale mam pytanie mam układ równań niejednorodny
3×1-x2+x3-x4=2
2×1-3×2-x3+x4=3
x1+7×3-6×4=5
Obliczyłem że r(W)=r(U)
i że r<n
i został mi taki układ równań
3×1-x2+x3=2+alfa
2×1-3×2-x3=3-alfa
x1+7×3=5+6alfa
Mogę to rozwiązać dalej cramerem?
Czy układ jednorodny może być sprzeczny ?
Dzięki za pytanie 🙂
Nie, nie może być. Będzie miał zawsze conajmniej jedno rozwiązanie – takie, w którym wszystkie zmienne równają się zero (rozwiązanie zerowe).
Mam nadzieje, ze moge liczyc na rozwiazanie ogolnie przykladowego rzedu macierzy..;)
1,3,-1,3=-1
2,7,0,1=2
-4,-14,0,-2=-4
Dobra.
Na wstępie doprecyzujmy, bo “rozwiązanie ogólne rzędu macierzy” to trochę pomieszanie pojęć, chodzi nam o “rozwiązanie ogólne UKŁADU RÓWNAŃ przy zastosowaniu rzędu macierzy” – prawda?
To jedziemy metodami z mojego Kursu Macierzy i z mojego Wykładu o liczeniu układów przy użyciu Twierdzenia Kroneckera – Capellego ).
Liczę rząd macierzy głównej:
Liczę rząd macierzy uzupełnionej:
Rzędy są sobie równe (zatem układ ma rozwiązania) i są równe 2. Bierzemy zatem macierz główną i wybieramy z niej “podmacierz” stopnia 2:
Jej wyznacznik jest różny od zera, czyli może być:
Tworzę nowy układ równań. Trzecie równanie, które nie załapało się do podmacierzy wywalam, a zmienne trzecią i czwartą (jak się kurka w ogóle nazywają zmienne w tym układzie? – zdecyduję się na [pmath]x_1,x_2,x_3,x_4[/pmath]) zastępuję parametrami [pmath]{alpha}_1,{alpha}_2[/pmath].
Mam więc układ:
No i skoro wyszedł taki prosty i tylko z dwoma niewiadomymi, nie rozwiązuję go wzorami Cramera, tylko metodami z gimnazjum:
Mam w ten sposób rozwiązanie ogólne układu:
Witam serdecznie, mam mały problem mam nadzieje, ze otrzymam tu pomoc 😉
Mianowicie, nie mam zielonego pojecia jak określić dokladnie ile wynosi rzad macierzy glownej a ile uzupełnionej, z tego co dowiedziałem się z tej stronki zależy to od ilości wierszy wiec potrafie określić ile rząd może wynosić maksymalnie ale nie wiem jak określic doklady wynik.
Witam, to trochę złożona sprawa, ale zapraszam do swojego Kursu:
https://etrapez.pl/produkt/kurs-macierze/
Na Lekcji 5 w prezentacjach Video tłumaczę tam, jak konkretnie obliczać rząd macierzy (ja to robię przez wykreślanie “wyzerowanych” wierszy lub/i kolumn).
Czym w takim razie jest układ niejednorodny?
To taki układ, który nie jest jednorodny 🙂 To znaczy, że ma co najmniej jedną liczbę różną od zera jako wyraz wolny.
Dziękuję, teraz wszystko zrozumiałem (przynajmniej takie odnoszę wrażenie). Chciałbym też podziękować Panu za prowadzenie tego bloga i za fragmenty kursów jakie pojawiły się na youtube. Sposób, w jaki przekazuje Pan wiedzę jest przystępny dla każdego i mimo niektórych uproszczeń (nieformalnych definicji) zawsze robi Pan to tak, aby zachować poprawność merytoryczną jakiegoś twierdzenia, wzoru. To jest świetne. Szkoda, że nie mam środków, aby wykupić całość kursów. Myślę, że to doskonała pomoc dla wszystkich chcących nauczyć się matematyki. A przede wszystkim ją zrozumieć.
Pozdrawiam
Dziękuję, pozdrawiam.
Wciąż mam problem z tym zdaniem:
“Jeżeli za wszystkie niewiadome w równaniach wstawimy zera widać jasno, że każde równanie układu jednorodnego będzie spełnione, zawsze i w każdym układzie jednorodnym.”
Bo dla układu jednorodnego
2x + 3y + 4z + 5t = 0
3x + 4t + 5z + 6t = 0
Wstawimy zero za każdą zmienną i mamy….? 😉
Ale skoro tak nie jest, to źle rozumiem.
Dzięki bardzo za pomoc!
“Wstawimy zero za każdą zmienną i mamy….? ;)”
…i mamy sprawdzenie, że rozwiązanie zerowe jest faktycznie rozwiązaniem tego układu 🙂
Trudno jednak nazwać takie “sprawdzenie” – “rozwiązaniem”.
“Rozwiązanie” to wartości zmiennych:
x=0
y=0
z=0
t=0
Równania, jakie powstaną po podstawieniu “rozwiązania” (w układzie jednorodnym każde równanie wtedy przyjmie postać 0=0) to NIE JEST “rozwiązanie”.
Dzięki za pytanie.
Nie, nie, nie – “rozwiązanie zerowe” to coś zupełnie innego.
Mając układ równań ze zmiennymi na przykład: x,y,z,t jego rozwiązanie to takie rozwiązanie, w którym:
x=0
y=0
z=0
t=0
Rozwiązanie “niezerowe” to było by na przykład rozwiązanie:
x=1
y=2
z=0
t=-5
Chodzi o to, że WSZYSTKIE wartości zmiennych spełniające układ równań muszą być równe 0 – wtedy rozwiązanie jest “zerowe”.
Sprawa jest jasna, czy mam trochę to rozwinąć?
Pomocy:Mam rozwiązać taki układ równań i mi w ogóle to nie wychodzi: x+2y-3z=42x+y+z=93x+3y-2z=13x-y+4z=5
Wobec tego, że
“Rozwiązaniem zerowym nazwiemy takie rozwiązanie, w którym wartości wszystkich niewiadomych równe są 0”,
to
czy jest to rozwiązanie postaci 0=0 w każdym wierszu macierzy (układu równań)?