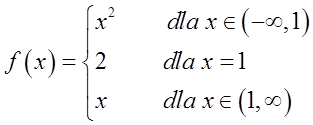
Dwa rodzaje punktów nieciągłości (granice funkcji)
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Ciągłość funkcji w punkcie
Jak wszyscy wiemy (chociażby z mojego Kursu Granic ) funkcja ![]() jest ciągła w punkcie
jest ciągła w punkcie ![]()
![]()
![]()
![]()
![]()
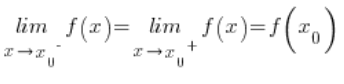
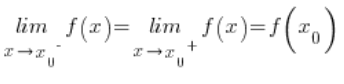
Czyli gdy granica lewostronna tej funkcji w tym punkcie równa jest granicy prawostronnej funkcji w tym punkcie równa jest wartości funkcji w tym punkcie.
Jeśli któraś z równości nie jest spełniona, funkcja ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
W tym nazywaniu można pójść krok dalej i ROZRÓŻNIĆ od siebie punkty nieciągłości. Robimy to tak:
Punkty nieciągłości I rodzaju
Punkt nieciągłości ![]()
![]()
![]()
![]()
![]()
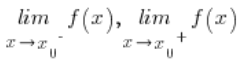
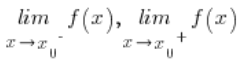
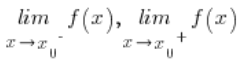
Dodatkowo, jeśli te granice są równe sobie, wtedy punkt nieciągłości I rodzaju nazywamy usuwalnym.
Punkty nieciągłości II rodzaju
Punkt nieciągłości ![]()
![]()
![]()
![]()
![]()
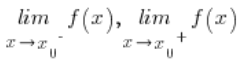
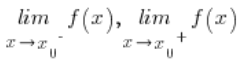
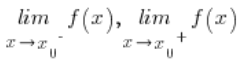
Przykład 1
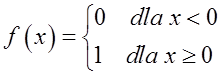
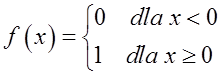
Ta funkcja ma w punkcie ![]()
![]()
![]()
Przykład 2
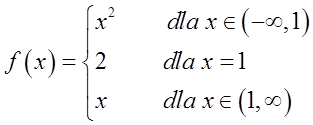
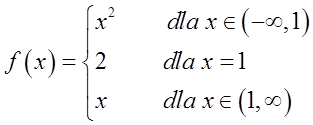
Ta funkcja ma w punkcie ![]()
![]()
Przykład 3
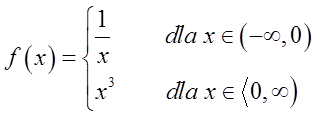
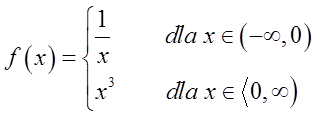
Ta funkcja ma w punkcie ![]()
![]()
![]()
![]()
![]()
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.










Wreszcie w jakiś logicczny sposob zostalo to wytlumaczone !!
DZIEKUJE!!
Witam.
Chciałam zapytać jak należy narysować punkt nieciągłości drugiego rodzaju na wykresie funkcji?
Witam!!
W książce analiza matematyczna Krysicki, Włodarski, jest parę takich zadań
piszę żeby zbadać ciągłość funkcji, jest podana funkcja np. f(x)=x+1/x ale niema podanych tych punktów.
Jak takie coś się liczy??
W tym przypadku wystarczy wyznaczyć dziedzinę. Funkcja oczywiście nie jest ciągła w punktach, które w ogóle nie należą do dziedziny.
W przypadku np. funkcji f\left( x \right)=x+\frac{1}{x}funkcja jest ciągła w przedziale R\backslash \{ 0 \}.
Zbiór liczb rzeczywistych z wyłączeniem zera to nie przedział tylko suma przedziałów!
Hej! A co jeśli w dziedzinie funkcji występuje np x>0 , x =0 ? Co z granicą prawostronną?
Hej! Chodzi o przedział dziedziny \left\langle 0,\infty \right)? x=0 nie jest wtedy na pewno wykresem asymptoty prawostronnej i jeśli funkcja nie istnieje na lewo od zera to nie jest również lewostronnej.
Ja miałbym do Pana takie pytanie z “innej beczki”. Czy da się w jakiś prosty sposób sprawdzać granice ciągów z definicj? Mam tu na myśli np. ciągi wymierne(z drugimi i trzecimi stopniami potęgi) i wykładnicze.